Walking Randomly

This is part 4 of a series of articles devoted to demonstrating how to call the Numerical Algorithms Group (NAG) C library from Python. Click here for the index to this series.

The NAG C library makes extensive use of C structures throughout its code base and so we will need to know how to represent them in Python.  For example, the NAG routine d01ajc is a general purpose one dimensional numerical integrator and one of it’s arguments is a structure called Nag_QuadProgress with the following prototype (found in the nag_types.h file that comes with the NAG C library)

  typedef struct
  {
    Integer num_subint;
    Integer fun_count;
    double *sub_int_beg_pts;
    double *sub_int_end_pts;
    double *sub_int_result;
    double *sub_int_error;
  } Nag_QuadProgress;

following the ctypes documentation on Structures and Unions, I came up with the following Python representation of this structure and it seems to work just fine.

class Nag_QuadProgress(Structure):
    _fields_ = [("num_subint", c_int),
                ("funcount", c_int),
		("sub_int_beg_pts",POINTER(c_double) ),
                ("sub_int_end_pts",POINTER(c_double)),
		("sub_int_result",POINTER(c_double)  ),
		("sub_int_error",POINTER(c_double)  )
		]

This is the only extra information we need in order to write a Python program that calculates the numerical approximation to an integral using the NAG routine d01ajc. Let’s calculate the integral of the function 4/(1.0+x*x) over the interval [0,1]. The code is as follows:

#!/usr/bin/env python
#Example 3 using NAG C library and ctypes
#d01ajc - one dimensional quadrature
#Mike Croucher - April 2008
#Concept introduced : Creating and using Python versions of structures such as Nag_QuadProgress
from ctypes import *
libnag = cdll.LoadLibrary("/opt/NAG/cllux08dgl/lib/libnagc_nag.so.8")

d01ajc = libnag.d01ajc
d01ajc.restype=None

class Nag_QuadProgress(Structure):
    _fields_ = [("num_subint", c_int),
                ("funcount", c_int),
		("sub_int_beg_pts",POINTER(c_double) ),
                ("sub_int_end_pts",POINTER(c_double)),
		("sub_int_result",POINTER(c_double)  ),
		("sub_int_error",POINTER(c_double)  )
		]

#define python function
def py_func(x):
	return 4./(1.0+x*x)

#create the prototype for the c callback function
C_FUNC = CFUNCTYPE(c_double,c_double )

#now create the c callback function
c_func = C_FUNC(py_func)

#set up the problem
a = c_double(0.0)
b = c_double(1.0)
nlimit = c_int(100)
epsr = c_double(0.00001)
ifail = c_int(0)

max_num_subint=c_int(200)
nlimit = c_int(0)
result=c_double(0.0)
epsabs= c_double(0.0)
epsrel=c_double(0.0001);
abserr=c_double(0.0);
qp=Nag_QuadProgress()

d01ajc(c_func,a,b,epsabs,epsrel,max_num_subint,byref(result) ,byref(abserr),byref(qp),ifail )
print "Approximation of integral= %s" %(result.value)
print "Number of function evaluations=%s" % qp.funcount
print "Number of subintervals used= %s" % qp.num_subint

Copy and paste (or download) this to a file called d01ajc.py, make it executable and run it by typing the following at a bash prompt.

chmod +x ./d01ajc.py
./d01ajc.py

If all has gone well then you should get following result

Approximation of integral= 3.14159265359
Number of function evaluations=21
Number of subintervals used= 1

Note that in order to create an instance of the Nag_QuadProgress structure I just do

qp=Nag_QuadProgress()

It is also useful to compare the C prototype of d01ajc

void nag_1d_quad_gen (double (*f)(double x),
double a, double b, double epsabs, double epsrel,
Integer max_num_subint, double *result, double *abserr,
Nag_QuadProgress *qp, NagError *fail)

with the way I called it in Python

d01ajc(c_func,a,b,epsabs,epsrel,max_num_subint,byref(result) ,byref(abserr),byref(qp),ifail )

Note how pointer arguments such as

double *abserr

are called as follows

byref(abserr)


Yet again I have cheated with the NagError parameter and just used c_int(0) instead of a proper NagError structure. NagError will be treated properly in a future article.

On this blog I usually write about Mathematics, Mathematical software, programming and  Linux but one of the reasons for choosing the name ‘Walking Randomly’ was to give me a license to talk about whatever tickled my fancy from time to time.  This is one of those times.

A group of three software developers have got together to try and make a game for the iPhone in 30 days from start to finish and they are blogging their progress over at www.30daygame.com.  Now I don’t have an iPhone and I am unlikely to get one so why am I mentioning this you may wonder?

Well, first of all the development team contains two people I know very well by reputation – Craig Rothwell and ZodTTD.  ZodTTD is a well known developer of emulators for systems such as the Playstation Portable, iPhone and Gp2x whereas Craig is the lead developer of a new, open source handheld system called the Pandora.

The second reason for my interest in this project is that I find this sort of blog inherently fascinating.  A couple of years ago there was a very similar kind of game development blog by a team calling themselves Lightworks Games for a Windows Mobile game called Cavemen.  The resulting game was great fun to play and won several awards and yet the team made very little money from it.

Finally, once this game has been released for the iPhone, it will be ported to the (as yet unreleased) Pandora and that is a machine I am very interested in.  Wolfram Demonstrations in the palm of your hand anyone?

Over at Wild about Math, Sol introduced pandigital fraction sums of the form

I call these sums pandigital because the left hand side contains every digit from 0-9 once and once only.  Sol challenged his readers to come up with more equations of this type and so I had a crack using Mathematica.

In order to keep the number of solutions down (and to keep them as close as possible to Sol’s original examples), I only considered sums with four terms – 2 of which were integers and 2 of which were fractions. In other words sums of the form

My next simplification was to only consider numerators and denominators of up to 2 digits each so fractions such as 123/456 were immediately out.  As you might expect, I also didn’t count trivial re-arrangements of the terms as separate solutions.

Finally, I didn’t insist that the fractions were written in their lowest terms so, for example, 38/76 is allowed even though it could be rewritten as 1/2.  Since one of Sol’s original examples contained such a fraction, I didn’t want to remove them.  This also meant that I allowed fractions that could be rewritten as integers such as 48/16.

Even with all of these restrictions in place I came up with 580 solutions!  One of which is

Interestingly, (unless I have made a mistake) it seems that if you insist on having fractions in their lowest terms then there are no solutions at all!

Does anyone out there have anything to add to this little problem?  Have I messed up and missed a solution or is one of my solutions incorrect?  Have I missed something obvious?  Are there more interesting variations?  Anything?

This is part 3 of a series of articles on how to use the NAG C Library with Python using the ctypes module.  Click here for the introduction and index to the series.

Now that we have seen how to call the simplest of NAG functions from Python, it is time to move on and consider callback functions.  If you don’t know what a callback function is then I think that the current version of the relevant Wikipedia article explains it well:

A callback is executable code that is passed as an argument to other code.

For example, say you want to want to find the zero of the function exp(-x)/x using a routine from the NAG library.  Your first step would be to create a function that evaluates exp(-x)/x for any given x.    You’ll later pass this function to the NAG routine to allow the routine to evaluate exp(-x)/x wherever it needs to.

Let’s take a look at some Python code that performs the calculation described above.  The NAG routine I am using locates a zero of a continuous function in a given interval by a combination of the methods of linear interpolation, extrapolation and bisection and is called c05adc.


#!/usr/bin/env python
#Example 2 using NAG C libray and ctypes
#Mike Croucher - April 2008
#Concept Introduced : Callback functions

from ctypes import *
from math import *
libnag = cdll.LoadLibrary("/opt/NAG/cllux08dgl/lib/libnagc_nag.so.8")

c05adc = libnag.c05adc
c05adc.restype=None


#define python function
def py_func(x):
     return exp(-x)-x


#create the type for the c callback function
C_FUNC = CFUNCTYPE(c_double,c_double )

#now create the c callback function
c_func = C_FUNC(py_func)

a=c_double(0.0)
b=c_double(1.0)
xtol=c_double(0.00001)
ftol=c_double(0.0)
x=c_double(0.0)
fail=c_int(0)

c05adc(a, b, byref(x), c_func, xtol, ftol, fail );

print "result = %s" % (x.value)

Copy and paste (or download) this to a file called c05adc.py, make it executable and run it by typing the following at a bash prompt.

chmod +x ./c05adc.py
./c05adc.py

If all has gone well then you should get following output

result = 0.567143306605

Most of the code above will be familiar to anyone who worked through part 1 of this series.  The first unfamiliar part might be

#define python function
def py_func(x):
     return exp(-x)-x

Which is nothing more than a standard Python function for calculating exp(-x)-x.

C_FUNC = CFUNCTYPE(c_double,c_double )


Here I have created a new C function prototype called C_FUNC by using the CFUNCTYPE function from the ctypes module. The general syntax of CFUNCTYPE is

CFUNCTYPE(return_type,input_arg1,input_arg2,input_arg3)

where the list of input arguments can be as long as you like.  The C function I want to create from my Python function should return a c_double and have a single c_double input argument so I end up with CFUNCTYPE(c_double,c_double )


c_func = C_FUNC(py_func)

Here I have used the function prototype created earlier to generate a C function called c_func based on my Python function py_func.

c05adc(a, b, byref(x), c_func, xtol, ftol, fail );

Finally, I call the NAG routine c05adc using all of the arguments set up earlier.   Note that I can pass my C function, c_func, to the NAG routine just as easily as I would any other argument. For reference, here is the original C prototype of the NAG routine along with a list of its arguments and what they mean

void nag_zero_cont_func_bd(double a, double b, double *x,
double (*f)(double x), double xtol,
double ftol, NagError *fail)


• a – (Input) The lower bound of the interval [a,b] in which the search for a zero will take place.
• b – (Input) The upper bound of the interval
• x – (Output) The approximation to the zero.  Note that the C prototype uses a pointer to double and I have emulated this in python using the byref() function to pass x by reference.
• f – (Input) A pointer to the function who’s zeros we want to find.  The C prototype might look complicated but, as you have seen, the implementation in Python is quite straightforward.
• xtol – (Input) The absolute tolerance to which the zero is required.
• ftol – (Input)  a value such that if |f (x)| < ftol, x is accepted as the zero.  ftol may be specified as0.0
• fail – The NAG error parameter.  We haven’t covered structures yet so we can’t use NAGError properly but I have used the trick that the NAG routines will accept c_int(0) in order to accept the default error handling behaviour.

That’s it for now. Next time I will be looking at numerical integration using the NAG library which will require the introduction of structures.

As always, comments, queries and corrections are gratefully received.

I have been playing around behind the scenes and have added a few small enhancements to Walking Randomly to try and make it more useful to readers.

New Search Box

The first update is the addition of a search box near the top left hand side of the page.   With over 220 individual posts, I was starting to struggle to find my own content so heaven knows how difficult the typical reader might find it.  I find the new search functionality quite useful and I hope you do too.

Latex in the comments

I have been using mimetex to typeset Mathematical equations ever since I started this blog and it has always worked well for me.  However, the version of the mimetex plugin-in I was using didn’t allow typeset equations in the comments section of posts which made it difficult for readers to post equations.

Well, after a bit of googling and experimentation, I figured out how to get it to work in comments as well.  It turned out that the php script only needed one extra line of code!

So, if you would like to put an equation in a comment all you need to do is write your Latex inside the tags you need to type [tex ] \light \int_0^1 x^2 [ /tex] but remember to remove the spaces from inside the [] tags.

That’s pretty much it.  After all they are only minor enhancements.

The Future – What do you want?

Feel free to let me know of anything else that you think I should do to improve things around here.  What do you like?  What don’t you like? What would you like to see more of?  Are there any topics you wish I would cover? I can’t promise that I’ll act on your suggestions but if you don’t ask you don’t get.

Thanks for reading and making blogging a worthwhile hobby for me.

A new version of the popular free, open source MATLAB clone, Octave, was released yesterday containing a fix to a bug introduced in the previous version, 3.0.4 which itself was only released last week containing yet more bug fixes.

Octave is a fantastic project and it’s great to see that the development team responds to bugs in the code so quickly.

I was discussing the (relatively) new Symbolic Toolbox for MATLAB with someone yesterday and found the need to trawl through the documentation.  There is a command called mfun in the symbolic toolbox which allows you to numerically evaluate various special functions such as Dawson’s integral or the digamma function.  Let’s look at the output of  help mfun in MATLAB 2009a.  The bold highlights are mine.

help mfun
MFUN   Numeric evaluation of a special function.
MFUN(‘fun’,p1,p2,…,pk), where ‘fun’ is the name of a Maple
function and the p’s are numeric quantities corresponding to fun’s
parameters.  The last parameter specified may be a matrix. All other
parameters must be the type specified by the Maple function.
MFUN numerically evaluates ‘fun’ with the specified parameters
and returns MATLAB doubles. Any singularity in ‘fun’ is returned
as NaN.

Of course, it should be MuPAD rather than Maple these days :-)  The text in the help browser is correct though and refers to MuPAD throughout.

What’s more if you do help mfunlist in MATLAB 2009a (to list all of the functions supported by mfun) then near the end of the list you’ll get the following extract

Orthogonal Polynomials (Extended Symbolic Math Toolbox only)
T      n,x             Chebyshev of the First Kind
U      n,x             Chebyshev of the Second Kind

However, the Extended Symbolic Toolbox was discontinued from MATLAB 2008b onwards and all of the Orthogonal Polynomials mentioned in the help file are now available in new symbolic toolbox as standard.

This is no big deal (Walking Randomly probably has MANY more typos than this for example) and after a change as major as swapping the Maple toolbox for the Mupad one I guess things such as this should be expected from time to time.

From time to time I post a problem of the week on Walking Randomly and invite readers to post solutions.  Although I haven’t done many, they seem to be quite popular and so I plan on resurrecting the series soon.

Back in August last year I posted a problem concerning Fibonacci numbers and matrices and Sam Shah (Of Continuous Everywhere but Differentiable Nowhere fame) took the time to write out a full solution in a PDF file and sent it to me via email.  I promised that I would publish it ‘soon’.

Well…umm…’soon’ turned out to be almost a year later.  Here is Sam’s solution to the original problem – enjoy!

Sorry Sam!

This is part 2 of a series of articles devoted to demonstrating how to call the Numerical Algorithms Group (NAG) C library from Python. Click here for the index to this series.

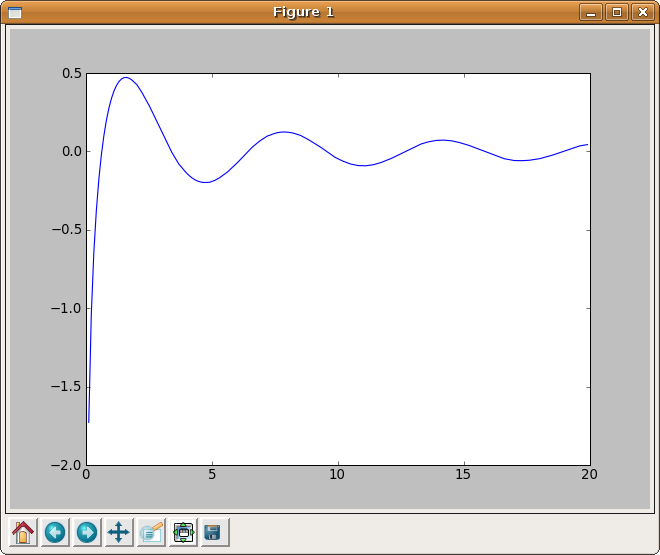
In part 1 I explained how to calculate the Cosine Integral, Ci(x), using Python and the NAG C library but the example code was a little dull in that it only calculated Ci(0.2).  Before moving onto more advanced topics I thought it would be fun to use the python module, matplotlib, to generate a plot of the cosine integral.

#!/usr/bin/env python
from ctypes import *
import matplotlib.pyplot as plt

libnag = cdll.LoadLibrary("/opt/NAG/cllux08dgl/lib/libnagc_nag.so.8")
s13acc = libnag.s13acc
s13acc.restype=c_double

fail=c_int(0)
def nag_cos_integral(x):
	x=c_double(x)
	result= s13acc(x,fail)
	return result

xvals = [x*0.1 for x in range(1,200)]
yvals = map(nag_cos_integral,xvals)

plt.plot(xvals,yvals)
plt.show()

Click here to download this program – you’ll need a copy of the NAG C library to make it work. The output is shown below.

Here is a combination I never thought I would see – using Mathematica to update your twitter account courtesy of code from James Rohal. I’ve not tried it yet but it looks like fun!

If you have never heard of Twitter I suggest you take a look at the Wikipedia article.  It’s a lot of fun and you’ll find people like  Stephen Fry and Barack Obama among its users.

Update (12th May2009): A little while after James posted his tutorial, Wolfram Research updated their blog with a more in-depth look at accessing Twitter from Mathematica.