Archive for June, 2010
MATLAB contains a function called pdist that calculates the ‘Pairwise distance between pairs of objects’. Typical usage is
X=rand(10,2); dists=pdist(X,'euclidean');
It’s a nice function but the problem with it is that it is part of the Statistics Toolbox and that costs extra. I was recently approached by a user who needed access to the pdist function but all of the statistics toolbox license tokens on our network were in use and this led to the error message
??? License checkout failed. License Manager Error -4 Maximum number of users for Statistics_Toolbox reached. Try again later. To see a list of current users use the lmstat utility or contact your License Administrator
One option, of course, is to buy more licenses for the statistics toolbox but there is another way. You may have heard of GNU Octave, a free,open-source MATLAB-like program that has been in development for many years. Well, Octave has a sister project called Octave-Forge which aims to provide a set of free toolboxes for Octave. It turns out that not only does Octave-forge contain a statistics toolbox but that toolbox contains an pdist function. I wondered how hard it would be to take Octave-forge’s pdist function and modify it so that it ran on MATLAB.
Not very! There is a script called oct2mat that is designed to automate some of the translation but I chose not to use it – I prefer to get my hands dirty you see. I named the resulting function octave_pdist to help clearly identify the fact that you are using an Octave function rather than a MATLAB function. This may matter if one or the other turns out to have bugs. It appears to work rather nicely:
dists_oct = octave_pdist(X,'euclidean');
% let's see if it agrees with the stats toolbox version
all( abs(dists_oct-dists)<1e-10)
ans =
1
Let’s look at timings on a slightly bigger problem.
>> X=rand(1000,2); >> tic;matdists=pdist(X,'euclidean');toc Elapsed time is 0.018972 seconds. >> tic;octdists=octave_pdist(X,'euclidean');toc Elapsed time is 6.644317 seconds.
Uh-oh! The Octave version is 350 times slower (for this problem) than the MATLAB version. Ouch! As far as I can tell, this isn’t down to my dodgy porting efforts, the original Octave pdist really does take that long on my machine (Ubuntu 9.10, Octave 3.0.5).
This was far too slow to be of practical use and we didn’t want to be modifying algorithms so we ditched this function and went with the NAG Toolbox for MATLAB instead (routine g03ea in case you are interested) since Manchester effectively has an infinite number of licenses for that product.
If,however, you’d like to play with my MATLAB port of Octave’s pdist then download it below.
- octave_pdist.m makes use of some functions in the excellent NaN Toolbox so you will need to download and install that package first.
One of the earliest posts I made on Walking Randomly (almost 3 years ago now – how time flies!) described the following equation and gave a plot of it in Mathematica.
![]()

Some time later I followed this up with another blog post and a Wolfram Demonstration.
Well, over at Stack Overflow, some people have been rendering this cool equation using MATLAB. Here’s the first version
x = linspace(-3,3,50); y = linspace(-5,5,50); [X Y]=meshgrid(x,y); Z = exp(-X.^2-Y.^2/2).*cos(4*X) + exp(-3*((X+0.5).^2+Y.^2/2)); Z(Z>0.001)=0.001; Z(Z<-0.001)=-0.001; surf(X,Y,Z); colormap(flipud(cool)) view([1 -1.5 2])

and here’s the second.
[x y] = meshgrid( linspace(-3,3,50), linspace(-5,5,50) );
z = exp(-x.^2-0.5*y.^2).*cos(4*x) + exp(-3*((x+0.5).^2+0.5*y.^2));
idx = ( abs(z)>0.001 );
z(idx) = 0.001 * sign(z(idx));
figure('renderer','opengl')
patch(surf2patch(surf(x,y,z)), 'FaceColor','interp');
set(gca, 'Box','on', ...
'XColor',[.3 .3 .3], 'YColor',[.3 .3 .3], 'ZColor',[.3 .3 .3], 'FontSize',8)
title('$e^{-x^2 - \frac{y^2}{2}}\cos(4x) + e^{-3((x+0.5)^2+\frac{y^2}{2})}$', ...
'Interpreter','latex', 'FontSize',12)
view(35,65)
colormap( [flipud(cool);cool] )
camlight headlight, lighting phong

Do you have any cool graphs to share?
Apple’s iPad hasn’t been available for very long but there is already a wealth of mathematical apps available for it and I expect the current crop to only be the tip of the iceberg. So, this is the beginning of a new series of articles on Walking Randomly where I’ll explore the options for doing mathematics on this new platform.
Update: Part 2 is now available
SpaceTime Mathematics
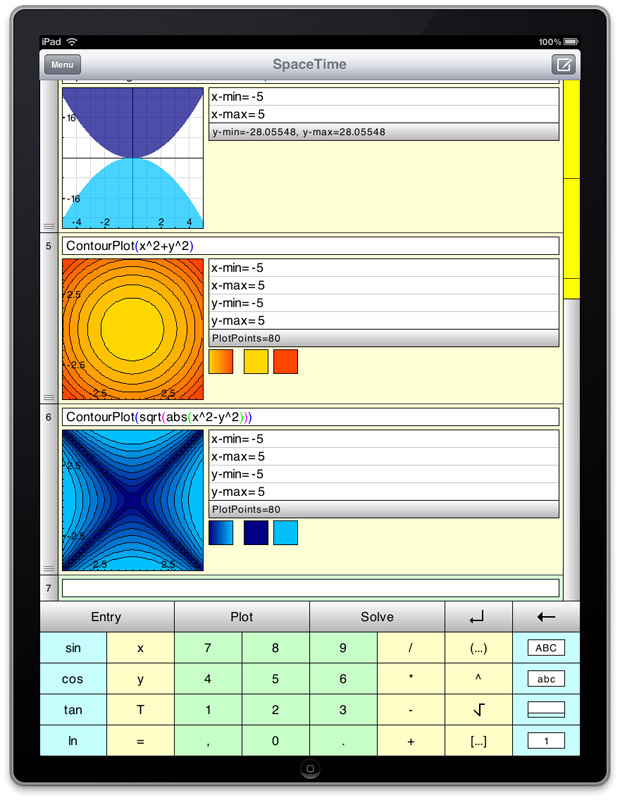
The Rolls Royce of mobile mathematical applications and one that I have been using since my days as a Windows Mobile user. The iPad version was one of the first apps I bought when I received my device and it is just beautiful! Symbolic algebra and calculus, 2 and 3D interactive plotting, scripting, fractals linear algebra…the list of functions just goes on and on. I would have loved to have access to this app when I was in high school or early university.
If you want to get an idea of the quality of SpaceTime’s graphical capabilities then check out the free demo, Graphbook, but be aware that there is a lot more to SpaceTime than just graphics.
Regular readers of Walking Randomly will know that I am a big fan of Wolfram’s Demonstration project which is made possible by Mathematica’s Manipulate function. Well, SpaceTime has a similar, albeit simplified, version of Manipulate – a function called Scroll. Interactive Fourier Series on the iPad anyone?
Something else that I like about SpaceTime is the fact that it is cross-platform with versions for Linux and Windows available in addition to iPhone, iPad and Windows Mobile. So, students could use it in a classroom setting on PCs and use what they have learned on their own iPad/iPhone version.
If you only buy one mathematical application for iPad then this should be it. It’s relatively expensive for an iPad app at £11.99 (at the time of writing) but is worth every penny and I bought it without hesitation – so should you!
PocketCAS Pro
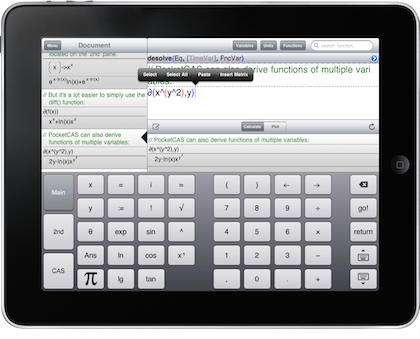
PocketCAS Pro is a computer algebra system that started out life as a Windows Mobile app and is now available for iPhone and iPad. I haven’t had chance to try it out yet so I can’t comment on its quality but it has a lot of features including symbolic algebra and calculus, 2D plotting, numerical solution of equations and more.
At the time of writing, it is the same price as SpaceTime mathematics – £11.99 – and yet my first impression is that it has less functionality. No 3d plotting for example. I’ll know more when I buy a copy next month.
There is a free lite version available which includes some of the functionality of the main product to allow you to try it out.
- PocketCAS Pro on iTunes.
- PocketCAS lite – free, cut down version of PocketCAS Pro
- PocketCAS main website
fxIntegrator

My favourite operating system is Linux where there is a philosophy of “Write programs that do one thing and do it well”. fxIntegrator does one thing -the numerical solution of 1d integrals – but does it do it well?
Well, it’s not bad. You enter the function you want to integrate using the nice, specially designed keyboard, then you enter the limits and press the = button to get the result. Couldn’t get any easier and I like it. The equation editor is very nice resulting in well formatted integrands but I did manage to confuse it once or twice. FxIntegrator is also very cheap at only 59p – a real bargain!
I tried a few straightforward integrals on it and it gave the correct answer in all cases. Then I got nasty and tried the following which has an algebraic-logarithmic singularity at the origin (original source for this integral).
![]()
I wasn’t expecting fxIntegrator to cope and it didn’t. Rather than giving the answer I just got an unhappy face indicating that it couldn’t compute the solution. This isn’t a criticism though! I like the fact that rather than giving numerical garbage, fxIntegator simply said ‘I can’t do that’.
There are some niggles, however. First of all, the list of elementary functions available is rather limited as it only includes square roots, powers,the trigonometric functions sin,cos and tan, the natural logarithm function ln and basic arithmetic. Even when I was in high school I would have wanted more such as inverse trig functions. (update: There are now a lot more functions including inverse trig)
Another problem with it is that although you can use the customised keyboard to enter the integrand, when you try to enter limits the standard iPad keyboard pops up.
These niggles aside, however, this is a nice little app for 59p and I hope the author continues to develop it. If he does then here are some suggestions for functionality I’d like to see.
- Add a few more functions. Inverse trig for a start. If possible then maybe things such as Bessel functions. (update: Inverse trig has now been added)
- Help turn this into a better teaching and learning tool by implementing a range of numerical methods for computing the integrand and allow the user to choose between them. Methods such as the rectangle rule, trapezoidal rule and simpson’s rule along with the ability to change the sub-divison size. The more methods the better :) (update: There are now three integration methods)
- Perhaps add some tutorial notes on each numerical method.
- Give the calculation time for the result in seconds along with the number of evaluations of the integrand. This will help students compare the trade off in speed/accuracy of each method. (update: This has now been done and looks great)
- Add the ability to plot the integrand along with the limits. Allow the user to change limits by moving them on the graph as well as by direct input. Once the calculation is performed, show the points on the curve where the algorithm sampled the function.
This good little app could be turned into a great little app.
Update (December 2010)
fxIntegrator has been updated several times since this article was written and it has improved even further. There are now three integration methods (Simpson, Trapeze and Rectangle) and several new functions have been implemented including inverse trig. Without doubt, this is now a great little app.
Update (February 2011)
More info on fxIntegrator. Of the version I originally reviewed I said “although you can use the customised keyboard to enter the integrand, when you try to enter limits the standard iPad keyboard pops up”. This is no longer the case in the current release. In fact, when entering the limits, not only you don’t see the standard iPad keyboard anymore, but you can freely write full-blown formulas (which can be just as complex as the integrands) to be used as integration limits. Further more, infinite limits are now possible too!
More articles from Walking Randomly on mobile Mathematics
Ever wondered how fast the fastest computer on Earth is? Well wonder no more because the latest edition of the Top 500 supercomputers was published earlier this week. Thanks to this list we can see that the fastest (publicly announced) computer in the world is currently an American system called Jaguar. Jaguar currently consists of 37,376 six-core AMD Istanbul processors and has a speed of 1.75 petaflops as measured by the Linpack benchmarks. According to the BBC, a computation that takes Jaguar a day would keep a standard desktop PC busy for 100 years. Whichever way you look at it, Jaguar is a seriously quick piece of kit.
All this got me thinking….how fast is my mobile phone compared to these computational behemoths?
The key to answering this question lies with the Linpack benchmarks developed by Jack Dongarra back in 1979. Wikipedia explains:
‘they [The Linpack benchmarks] measure how fast a computer solves a dense N by N system of linear equations Ax = b, which is a common task in engineering. The solution is obtained by Gaussian elimination with partial pivoting, with 2/3·N3 + 2·N2 floating point operations. The result is reported in millions of floating point operations per second (MFLOP/s).’
People have been using the Linpack benchmarks to measure the speed of computers for decades and so we can use the historical results to see just how far computers have come over the last thirty years or so. Back in 1979, for example, the fastest computer on the block according to the N=100 Linpack benchmark was the Cray 1 supercomputer which had a measured speed of 3.4 Mflop/s per processor.
More recently, a Java version of the Linpack benchmark was developed and this was used by GreeneComputing to produce an Android version of the benchmark.

I installed the benchmark onto my trusty T-Mobile G2 (a rebadged HTC Hero, currently running Android 1.5) and on firing it up discovered that it tops out at around 2.3 Mflop/s which makes it around 66% as fast as a single processor on a 1979 Cray 1 supercomputer. OK, so maybe that’s not particularly impressive but the very latest crop of Android phones are a different matter entirely.
According to the current Top 10 Android Linpack results, a tweaked Motorola Droid is capable of scoring 52 Mflop/s which is over 15 times faster than the 1979 Cray 1 CPU. Put another way, if you transported that mobile phone back to 1987 then it would be on par with the processors in one of the fastest computers in the world of the time, the ETA 10-E, and they had to be cooled by liquid nitrogen.
Like all benchmarks, however, you need to take this one with a pinch of salt. As explained on the Java Linpack page ‘This [the Java version of the] test is more a reflection of the state of the Java systems than of the floating point performance of the underlying processors.’ In other words, the underlying processors of our mobile phones are probably faster than these Java based tests imply.
