Archive for October, 2010
Some time ago now, Sam Shah of Continuous Everywhere but Differentiable Nowhere fame discussed the standard method of obtaining the square root of the imaginary unit, i, and in the ensuing discussion thread someone asked the question “What is i^i – that is what is i to the power i?”
Sam immediately came back with the answer e^(-pi/2) = 0.207879…. which is one of the answers but as pointed out by one of his readers, Adam Glesser, this is just one of the infinite number of potential answers that all have the form e^{-(2k+1) pi/2} where k is an integer. Sam’s answer is the principle value of i^i (incidentally this is the value returned by google calculator if you google i^i – It is also the value returned by Mathematica and MATLAB). Life gets a lot more complicated when you move to the complex plane but it also gets a lot more interesting too.
While on the train into work one morning I was thinking about Sam’s blog post and wondered what the principal value of i^i^i (i to the power i to the power i) was equal to. Mathematica quickly provided the answer:
N[I^I^I] 0.947159+0.320764 I
So i is imaginary, i^i is real and i^i^i is imaginary again. Would i^i^i^i be real I wondered – would be fun if it was. Let’s see:
N[I^I^I^I] 0.0500922+0.602117 I
gah – a conjecture bites the dust – although if I am being honest it wasn’t a very good one. Still, since I have started making ‘power towers’ I may as well continue and see what I can see. Why am I calling them power towers? Well, the calculation above could be written as follows:
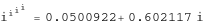
As I add more and more powers, the left hand side of the equation will tower up the page….Power Towers. We now have a sequence of the first four power towers of i:
i = i i^i = 0.207879 i^i^i = 0.947159 + 0.32076 I i^i^i^i = 0.0500922+0.602117 I
Sequences of power towers
“Will this sequence converge or diverge?”, I wondered. I wasn’t in the mood to think about a rigorous mathematical proof, I just wanted to play so I turned back to Mathematica. First things first, I needed to come up with a way of making an arbitrarily large power tower without having to do a lot of typing. Mathematica’s Nest function came to the rescue and the following function allows you to create a power tower of any size for any number, not just i.
tower[base_, size_] := Nest[N[(base^#)] &, base, size]
Now I can find the first term of my series by doing
In[1]:= tower[I, 0] Out[1]= I
Or the 5th term by doing
In[2]:= tower[I, 4] Out[2]= 0.387166 + 0.0305271 I
To investigate convergence I needed to create a table of these. Maybe the first 100 towers would do:
ColumnForm[
Table[tower[I, n], {n, 1, 100}]
]
The last few values given by the command above are
0.438272+ 0.360595 I 0.438287+ 0.360583 I 0.438287+ 0.3606 I 0.438275+ 0.360591 I 0.438289+ 0.360588 I
Now this is interesting – As I increased the size of the power tower, the result seemed to be converging to around 0.438 + 0.361 i. Further investigation confirms that the sequence of power towers of i converges to 0.438283+ 0.360592 i. If you were to ask me to guess what I thought would happen with large power towers like this then I would expect them to do one of three things – diverge to infinity, stay at 1 forever or quickly converge to 0 so this is unexpected behaviour (unexpected to me at least).
They converge, but how?
My next thought was ‘How does it converge to this value? In other words, ‘What path through the complex plane does this sequence of power towers take?” Time for a graph:
tower[base_, size_] := Nest[N[(base^#)] &, base, size];
complexSplit[x_] := {Re[x], Im[x]};
ListPlot[Map[complexSplit, Table[tower[I, n], {n, 0, 49, 1}]],
PlotRange -> All]
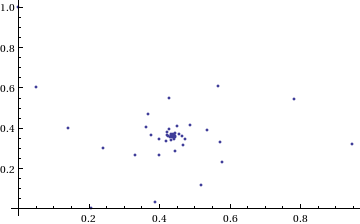
Who would have thought you could get a spiral from power towers? Very nice! So the next question is ‘What would happen if I took a different complex number as my starting point?’ For example – would power towers of (0.5 + i) converge?’
The answer turns out to be yes – power towers of (0.5 + I) converge to 0.541199+ 0.40681 I but the resulting spiral looks rather different from the one above.
tower[base_, size_] := Nest[N[(base^#)] &, base, size];
complexSplit[x_] := {Re[x], Im[x]};
ListPlot[Map[complexSplit, Table[tower[0.5 + I, n], {n, 0, 49, 1}]],
PlotRange -> All]
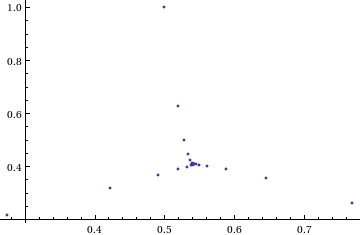The zoo of power tower spirals
So, taking power towers of two different complex numbers results in two qualitatively different ‘convergence spirals’. I wondered how many different spiral types I might find if I consider the entire complex plane? I already have all of the machinery I need to perform such an investigation but investigation is much more fun if it is interactive. Time for a Manipulate
complexSplit[x_] := {Re[x], Im[x]};
tower[base_, size_] := Nest[N[(base^#)] &, base, size];
generatePowerSpiral[p_, nmax_] :=
Map[complexSplit, Table[tower[p, n], {n, 0, nmax-1, 1}]];
Manipulate[const = p[[1]] + p[[2]] I;
ListPlot[generatePowerSpiral[const, n],
PlotRange -> {{-2, 2}, {-2, 2}}, Axes -> ax,
Epilog -> Inset[Framed[const], {-1.5, -1.5}]], {{n, 100,
"Number of terms"}, 1, 200, 1,
Appearance -> "Labeled"}, {{ax, True, "Show axis"}, {True,
False}}, {{p, {0, 1.5}}, Locator}]
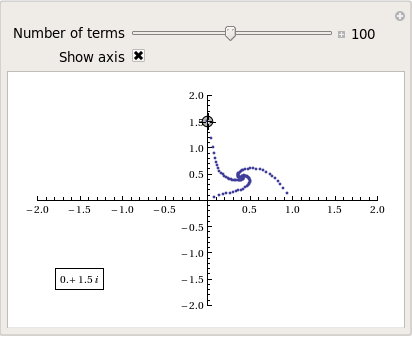
After playing around with this Manipulate for a few seconds it became clear to me that there is quite a rich diversity of these convergence spirals. Here are a couple more
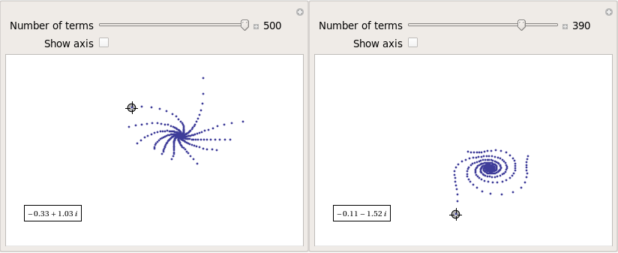
Some of them take a lot longer to converge than others and then there are those that don’t converge at all:
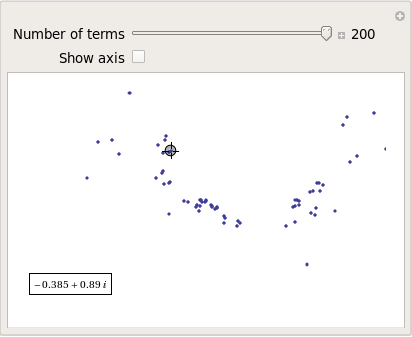
Optimising the code a little
Before I could investigate convergence any further, I had a problem to solve: Sometimes the Manipulate would completely freeze and a message eventually popped up saying “One or more dynamic objects are taking excessively long to finish evaluating……” What was causing this I wondered?
Well, some values give overflow errors:
In[12]:= generatePowerSpiral[-1 + -0.5 I, 200] General::ovfl: Overflow occurred in computation. >> General::ovfl: Overflow occurred in computation. >> General::ovfl: Overflow occurred in computation. >> General::stop: Further output of General::ovfl will be suppressed during this calculation. >>
Could errors such as this be making my Manipulate unstable? Let’s see how long it takes Mathematica to deal with the example above
AbsoluteTiming[ListPlot[generatePowerSpiral[-1 -0.5 I, 200]]]
On my machine, the above command typically takes around 0.08 seconds to complete compared to 0.04 seconds for a tower that converges nicely; it’s slower but not so slow that it should break Manipulate. Still, let’s fix it anyway.
Look at the sequence of values that make up this problematic power tower
generatePowerSpiral[-0.8 + 0.1 I, 10]
{{-0.8, 0.1}, {-0.668442, -0.570216}, {-2.0495, -6.11826},
{2.47539*10^7,1.59867*10^8}, {2.068155430437682*10^-211800874,
-9.83350984373519*10^-211800875}, {Overflow[], 0}, {Indeterminate,
Indeterminate}, {Indeterminate, Indeterminate}, {Indeterminate,
Indeterminate}, {Indeterminate, Indeterminate}}
Everything is just fine until the term {Overflow[],0} is reached; after which we are just wasting time. Recall that the functions I am using to create these sequences are
complexSplit[x_] := {Re[x], Im[x]};
tower[base_, size_] := Nest[N[(base^#)] &, base, size];
generatePowerSpiral[p_, nmax_] :=
Map[complexSplit, Table[tower[p, n], {n, 0, nmax-1, 1}]];
The first thing I need to do is break out of tower’s Nest function as soon as the result stops being a complex number and the NestWhile function allows me to do this. So, I could redefine the tower function to be
tower[base_, size_] := NestWhile[N[(base^#)] &, base, MatchQ[#, _Complex] &, 1, size]
However, I can do much better than that since my code so far is massively inefficient. Say I already have the first n terms of a tower sequence; to get the (n+1)th term all I need to do is a single power operation but my code is starting from the beginning and doing n power operations instead. So, to get the 5th term, for example, my code does this
I^I^I^I^I
instead of
(4th term)^I
The function I need to turn to is yet another variant of Nest – NestWhileList
fasttowerspiral[base_, size_] := Quiet[Map[complexSplit, NestWhileList[N[(base^#)] &, base, MatchQ[#, _Complex] &, 1, size, -1]]];
The Quiet function is there to prevent Mathematica from warning me about the Overflow error. I could probably do better than this and catch the Overflow error coming before it happens but since I’m only mucking around, I’ll leave that to an interested reader. For now it’s enough for me to know that the code is much faster than before:
(*Original Function*)
AbsoluteTiming[generatePowerSpiral[I, 200];]
{0.036254, Null}
(*Improved Function*)
AbsoluteTiming[fasttowerspiral[I, 200];]
{0.001740, Null}
A factor of 20 will do nicely!
Making Mathematica faster by making it stupid
I’m still not done though. Even with these optimisations, it can take a massive amount of time to compute some of these power tower spirals. For example
spiral = fasttowerspiral[-0.77 - 0.11 I, 100];
takes 10 seconds on my machine which is thousands of times slower than most towers take to compute. What on earth is going on? Let’s look at the first few numbers to see if we can find any clues
In[34]:= spiral[[1 ;; 10]]
Out[34]= {{-0.77, -0.11}, {-0.605189, 0.62837}, {-0.66393,
7.63862}, {1.05327*10^10,
7.62636*10^8}, {1.716487392960862*10^-155829929,
2.965988537183398*10^-155829929}, {1., \
-5.894184073663391*10^-155829929}, {-0.77, -0.11}, {-0.605189,
0.62837}, {-0.66393, 7.63862}, {1.05327*10^10, 7.62636*10^8}}
The first pair that jumps out at me is {1.71648739296086210^-155829929, 2.96598853718339810^-155829929} which is so close to {0,0} that it’s not even funny! So close, in fact, that they are not even double precision numbers any more. Mathematica has realised that the calculation was going to underflow and so it caught it and returned the result in arbitrary precision.
Arbitrary precision calculations are MUCH slower than double precision ones and this is why this particular calculation takes so long. Mathematica is being very clever but its cleverness is costing me a great deal of time and not adding much to the calculation in this case. I reckon that I want Mathematica to be stupid this time and so I’ll turn off its underflow safety net.
SetSystemOptions["CatchMachineUnderflow" -> False]
Now our problematic calculation takes 0.000842 seconds rather than 10 seconds which is so much faster that it borders on the astonishing. The results seem just fine too!
When do the power towers converge?
We have seen that some towers converge while others do not. Let S be the set of complex numbers which lead to convergent power towers. What might S look like? To determine that I have to come up with a function that answers the question ‘For a given complex number z, does the infinite power tower converge?’ The following is a quick stab at such a function
convergeQ[base_, size_] :=
If[Length[
Quiet[NestWhileList[N[(base^#)] &, base, Abs[#1 - #2] > 0.01 &,
2, size, -1]]] < size, 1, 0];
The tolerance I have chosen, 0.01, might be a little too large but these towers can take ages to converge and I’m more interested in speed than accuracy right now so 0.01 it is. convergeQ returns 1 when the tower seems to converge in at most size steps and 0 otherwise.:
In[3]:= convergeQ[I, 50] Out[3]= 1 In[4]:= convergeQ[-1 + 2 I, 50] Out[4]= 0
So, let’s apply this to a section of the complex plane.
towerFract[xmin_, xmax_, ymin_, ymax_, step_] :=
ArrayPlot[
Table[convergeQ[x + I y, 50], {y, ymin, ymax, step}, {x, xmin, xmax,step}]]
towerFract[-2, 2, -2, 2, 0.1]
That looks like it might be interesting, possibly even fractal, behaviour but I need to increase the resolution and maybe widen the range to see what’s really going on. That’s going to take quite a bit of calculation time so I need to optimise some more.
Going Parallel
There is no point in having machines with two, four or more processor cores if you only ever use one and so it is time to see if we can get our other cores in on the act.
It turns out that this calculation is an example of a so-called embarrassingly parallel problem and so life is going to be particularly easy for us. Basically, all we need to do is to give each core its own bit of the complex plane to work on, collect the results at the end and reap the increase in speed. Here’s the full parallel version of the power tower fractal code
(*Complete Parallel version of the power tower fractal code*)
convergeQ[base_, size_] :=
If[Length[
Quiet[NestWhileList[N[(base^#)] &, base, Abs[#1 - #2] > 0.01 &,
2, size, -1]]] < size, 1, 0];
LaunchKernels[];
DistributeDefinitions[convergeQ];
ParallelEvaluate[SetSystemOptions["CatchMachineUnderflow" -> False]];
towerFractParallel[xmin_, xmax_, ymin_, ymax_, step_] :=
ArrayPlot[
ParallelTable[
convergeQ[x + I y, 50], {y, ymin, ymax, step}, {x, xmin, xmax, step}
, Method -> "CoarsestGrained"]]
This code is pretty similar to the single processor version so let’s focus on the parallel modifications. My convergeQ function is no different to the serial version so nothing new to talk about there. So, the first new code is
LaunchKernels[];
This launches a set of parallel Mathematica kernels. The amount that actually get launched depends on the number of cores on your machine. So, on my dual core laptop I get 2 and on my quad core desktop I get 4.
DistributeDefinitions[convergeQ];
All of those parallel kernels are completely clean in that they don’t know about my user defined convergeQ function. This line sends the definition of convergeQ to all of the freshly launched parallel kernels.
ParallelEvaluate[SetSystemOptions["CatchMachineUnderflow" -> False]];
Here we turn off Mathematica’s machine underflow safety net on all of our parallel kernels using the ParallelEvaluate function.
That’s all that is necessary to set up the parallel environment. All that remains is to change Map to ParallelMap and to add the argument Method -> “CoarsestGrained” which basically says to Mathematica ‘Each sub-calculation will take a tiny amount of time to perform so you may as well send each core lots to do at once’ (click here for a blog post of mine where this is discussed further).
That’s all it took to take this embarrassingly parallel problem from a serial calculation to a parallel one. Let’s see if it worked. The test machine for what follows contains a T5800 Intel Core 2 Duo CPU running at 2Ghz on Ubuntu (if you want to repeat these timings then I suggest you read this blog post first or you may find the parallel version going slower than the serial one). I’ve suppressed the output of the graphic since I only want to time calculation and not rendering time.
(*Serial version*)
In[3]= AbsoluteTiming[towerFract[-2, 2, -2, 2, 0.1];]
Out[3]= {0.672976, Null}
(*Parallel version*)
In[4]= AbsoluteTiming[towerFractParallel[-2, 2, -2, 2, 0.1];]
Out[4]= {0.532504, Null}
In[5]= speedup = 0.672976/0.532504
Out[5]= 1.2638
I was hoping for a bit more than a factor of 1.26 but that’s the way it goes with parallel programming sometimes. The speedup factor gets a bit higher if you increase the size of the problem though. Let’s increase the problem size by a factor of 100.
towerFractParallel[-2, 2, -2, 2, 0.01]
The above calculation took 41.99 seconds compared to 63.58 seconds for the serial version resulting in a speedup factor of around 1.5 (or about 34% depending on how you want to look at it).
Other optimisations
I guess if I were really serious about optimising this problem then I could take advantage of the symmetry along the x axis or maybe I could utilise the fact that if one point in a convergence spiral converges then it follows that they all do. Maybe there are more intelligent ways to test for convergence or maybe I’d get a big speed increase from programming in C or F#? If anyone is interested in having a go at improving any of this and succeeds then let me know.
I’m not going to pursue any of these or any other optimisations, however, since the above exploration is what I achieved in a single train journey to work (The write-up took rather longer though). I didn’t know where I was going and I only worried about optimisation when I had to. At each step of the way the code was fast enough to ensure that I could interact with the problem at hand.
Being mostly ‘fast enough’ with minimal programming effort is one of the reasons I like playing with Mathematica when doing explorations such as this.
Treading where people have gone before
So, back to the power tower story. As I mentioned earlier, I did most of the above in a single train journey and I didn’t have access to the internet. I was quite excited that I had found a fractal from such a relatively simple system and very much felt like I had discovered something for myself. Would this lead to something that was publishable I wondered?
Sadly not!
It turns out that power towers have been thoroughly investigated and the act of forming a tower is called tetration. I learned that when a tower converges there is an analytical formula that gives what it will converge to:
Where W is the Lambert W function (click here for a cool poster for this function). I discovered that other people had already made Wolfram Demonstrations for power towers too
There is even a website called tetration.org that shows ‘my’ fractal in glorious technicolor. Nothing new under the sun eh?
Parting shots
Well, I didn’t discover anything new but I had a bit of fun along the way. Here’s the final Manipulate I came up with
Manipulate[const = p[[1]] + p[[2]] I;
If[hz,
ListPlot[fasttowerspiral[const, n], PlotRange -> {{-2, 2}, {-2, 2}},
Axes -> ax,
Epilog -> {{PointSize[Large], Red,
Point[complexSplit[N[h[const]]]]}, {Inset[
Framed[N[h[const]]], {-1, -1.5}]}}]
, ListPlot[fasttowerspiral[const, n],
PlotRange -> {{-2, 2}, {-2, 2}}, Axes -> ax]
]
, {{n, 100, "Number of terms"}, 1, 500, 1, Appearance -> "Labeled"}
, {{ax, True, "Show axis"}, {True, False}}
, {{hz, True, "Show h(z)"}, {True, False}}
, {{p, {0, 1.5}}, Locator}
, Initialization :> (
SetSystemOptions["CatchMachineUnderflow" -> False];
complexSplit[x_] := {Re[x], Im[x]};
fasttowerspiral[base_, size_] :=
Quiet[Map[complexSplit,
NestWhileList[N[(base^#)] &, base, MatchQ[#, _Complex] &, 1,
size, -1]]];
h[z_] := -ProductLog[-Log[z]]/Log[z];
)
]
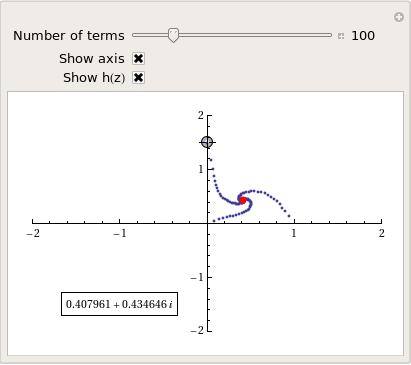
and here’s a video of a zoom into the tetration fractal that I made using spare cycles on Manchester University’s condor pool.
If you liked this blog post then you may also enjoy:
I was having a quick browse through the current Top-500 supercomputer list and it appears to me that UK Universities hardly feature at all. We’ve got Hector at Edinburgh University in at number 26 but that’s the UK’s National facility so we’d expect it to be good.
Other than that, we have The University of Southampton at Number 83, The University of Bristol at Number 378 and that seems to be about it (please correct me if I’m wrong). There are a few more UK-based installations in the top-500 but none of them are in Universities as far as I can tell.
I’m a little surprised by this since I thought that we (UK academia) would give a better account of ourselves. Does it matter that we don’t have more boxes in the top-500 within UK Academia? Is everyone doing research on smaller scale Beowulf clusters, condor pools, GP-GPUs and fully tricked-out 12 core desktops these days? Is the need for big boxes receding? Any insight anyone?
Because I spend so much time talking about and helping people with MATLAB, I often get asked to recommend a good MATLAB book. I actually find this a rather difficult question to answer because, contrary to what people seem to expect, I have a relatively small library of MATLAB books.
However, one could argue the fact that I only have a small library of books suggests that I hit upon the good ones straight away. So, for those in the market for an introductory MATLAB book, here are my recommendations
MATLAB Guide by Desmond and Nicholas Higham
If you only ever buy one MATLAB book then this should be it. It starts off with a relatively fast paced mini-tutorial that could be considered a sight-seeing tour of MATLAB and its functionality. Once this is done, the authors get down to the business of teaching you the fundamentals of MATLAB in a systematic,thorough and enjoyable manner.
Unlike some books I have seen, this one doesn’t just show you MATLAB syntax; instead it shows you how to be a good MATLAB programmer from the beginning. Your programs will be efficient, robust and well documented because you will know how to leverage MATLAB’s particular strengths.
One aspect of the Higham’s book that I particularly like is that they include many mathematical examples that are intrinsically interesting in their own right. This was where I first learned of Maurer roses, Viswanath’s constant and eigenvalue roulette for example. Systems such as MATLAB are ideal for demonstrating cool little mathematical ideas and so it’s great to see so many of them sprinkled throughout an introductory textbook such as this one.
The only downside to the current edition is that the chapter on the symbolic toolbox is out of date since it refers to the old Maple based one rather than the current Mupad based system (See my post here for more details on this transition). This is only a minor gripe, however, and I only really mention it at all in an attempt to give a review that looks more balanced.
Full disclosure: One of the authors, Nicholas Higham, works at the same university as me. However, we are in different departments and I paid for my own copy of his book in full.
MATLAB: A Practical Introduction to Programming and Problem Solving by Stormy Attaway
I haven’t had this book as long as I’ve had the Higham book and I haven’t even completely finished it yet. I am, however, very impressed with it (as an aside, it’s also the first technical book I ever bought using the iPad and Android Kindle apps).
One of the key things that I like most about this one is that the text is liberally sprinkled with ‘Quick Questions’ that give you a little scenario and ask you how you’d deal with it in MATLAB. This is quickly followed by a model answer that explains the concepts. These help break up the text, make you stop and think and ultimately lead to you thinking in a more MATLABy way. There is also a good amount of exercises at the end of each chapter (no model solutions provided though).
The book is split into two main parts with the first half concentrating on MATLAB fundamentals such as matrices, vectorization, strings, functions etc while the second half covers mathematical applications such as statistics, curve fitting and numerical integration. So, it’ll take you from being a complete novice to someone who knows their way around a reasonable portion of the system.
Since I first bought this book using the Kindle app on my iPad I thought I’d quickly mention how that worked out for me. In short, I hated the Kindle presentation so much that I went out and bought the physical version of the book as well. The paper version is beautifully formatted and presented whereas the Kindle version is just awful. It’s hard to navigate, looks awful and basically makes one wish that they had just given you a pdf file instead!
MATLAB has a command called reshape that,obviously enough, allows you to reshape a matrix.
mat=rand(4)
mat =
0.1576 0.8003 0.7922 0.8491
0.9706 0.1419 0.9595 0.9340
0.9572 0.4218 0.6557 0.6787
0.4854 0.9157 0.0357 0.7577
>> reshape(mat,[2,8])
ans =
0.1576 0.9572 0.8003 0.4218 0.7922 0.6557 0.8491 0.6787
0.9706 0.4854 0.1419 0.9157 0.9595 0.0357 0.9340 0.7577
Obviously, the number of rows and columns both have to be positive. A negative number of rows and columns makes no sense at all. On MATLAB 2010a:
>> reshape(mat,[-2,-8]) ??? Error using ==> reshape Size vector elements should be nonnegative.
So far so boring. However, I found an old copy of MATLAB on my system (version 6.5.1) which gives much more interesting error messages
>> reshape(mat,[-2,-8]) ??? Error using ==> reshape Don't do this again!.
Obviously, I ignore the warning
>> reshape(mat,[-2,-8]) ??? Error using ==> reshape Cleve says you should be doing something more useful.
Nope, I’ve got nothing better to do
??? Error using ==> reshape Seriously, size arguments cannot be negative.
I don’t know about you but I prefer the old error messages myself. MATLAB hasn’t completely lost its sense of humour, however, try evaluating the following for example
spy
Lots of people are hitting Walking Randomly looking for info about Mathematica 8 and have had to walk away disappointed….until now!
I’ve been part of the Mathematica 8 beta program for a while now and in order to access the goodies I had to sign an NDA which can be roughly summed up as ‘The first rule of Mathematica 8 beta is that you don’t talk about Mathematica 8 beta.’
As of today, however, I am allowed to show you a tiny little bit of it in advance of it being released. Mathematica 8 will include a massive amount of support for control theory. Here’s a brief preview
Let’s start by building a transfer function model
myTF = TransferFunctionModel[1/(1 + 2 s + 2 s^2 + s^3), s]
I can find its poles exactly
TransferFunctionPoles[myTF]
{{{-1, -(-1)^(1/3), (-1)^(2/3)}}}
and, of course, numerically
TransferFunctionPoles[myTF] //N
{{{-1., -0.5 - 0.866025 I, -0.5 + 0.866025 I}}}
Here’s its bode plot
BodePlot[myTF]
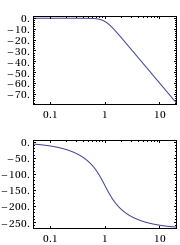
Here’s its response to a unit step function
stepresponse = OutputResponse[myTF, UnitStep[t], t]
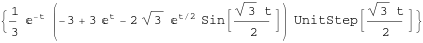
Let’s plot that response
Plot[stepresponse, {t, 0, 10}]
Finally, I convert it to a state space model.
StateSpaceModel[myTF]
That’s the tip of a very big iceberg ;)
Update: Mathematica 8 has now been released. See https://www.walkingrandomly.com/?p=3018 for more details.
Other Mathematica 8 previews
I work at The University of Manchester in the UK and, as some of you may have heard, two of our Professors recently won the Nobel Prize in physics for their discovery of graphene. Naturally, I wanted to learn more about graphene and, as a fan of Mathematica, I turned to the Wolfram Demonstrations Project to see what I could see. Click on the images to go to the relevant demonstration.
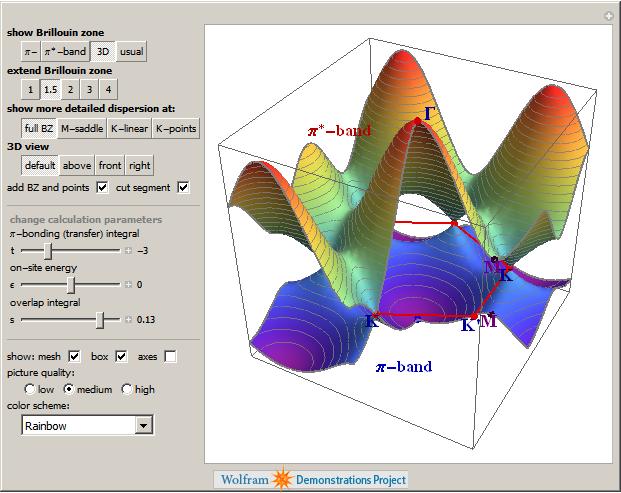
Back when I used to do physics research myself, I was interested in band structure and it turns out that there is a great demonstration from Vladimir Gavryushin that will help you learn all about the band structure of graphene using the tight binding approximation.
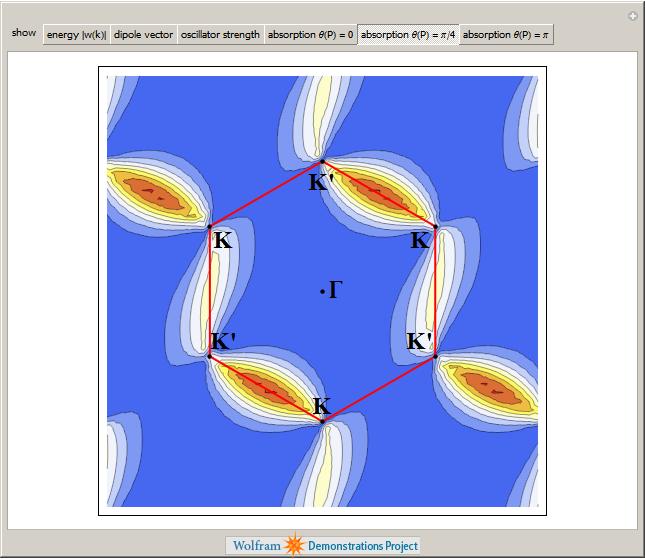
The electronic band structure of a material is important because it helps us to understand (and maybe even engineer) its electronic and optical properties and if you want to know more about its optical properties then the next demonstration from Jessica Alfonsi is for you.
Another professor at Manchester, Niels Walet, produced the next demonstration which asks “Is there a Klein Paradox in Graphene?”
Finally, Graphene can be rolled up to make Carbon Nanotubes as demonstrated by Sándor Kabai.
This is just a taster of the Graphene related demonstrations available at The Wolfram Demonstrations project (There are 11 at the time of writing) and I have no doubt that there will be more in the future. Many of them are exceptionally well written and they include lists of references, full source code and, best of all, they can be run for free using the Mathematica Player.
Don’t just read about cutting-edge research, get in there and interact with it!
Not long after publishing my article, A faster version of MATLAB’s fsolve using the NAG Toolbox for MATLAB, I was contacted by Biao Guo of Quantitative Finance Collector who asked me what I could do with the following piece of code.
function MarkowitzWeight = fsolve_markowitz_MATLAB()
RandStream.setDefaultStream (RandStream('mt19937ar','seed',1));
% simulate 500 stocks return
SimR = randn(1000,500);
r = mean(SimR); % use mean return as expected return
targetR = 0.02;
rCOV = cov(SimR); % covariance matrix
NumAsset = length(r);
options=optimset('Display','off');
startX = [1/NumAsset*ones(1, NumAsset), 1, 1];
x = fsolve(@fsolve_markowitz,startX,options, r, targetR, rCOV);
MarkowitzWeight = x(1:NumAsset);
end
function F = fsolve_markowitz(x, r, targetR, rCOV)
NumAsset = length(r);
F = zeros(1,NumAsset+2);
weight = x(1:NumAsset); % for asset weights
lambda = x(NumAsset+1);
mu = x(NumAsset+2);
for i = 1:NumAsset
F(i) = weight(i)*sum(rCOV(i,:))-lambda*r(i)-mu;
end
F(NumAsset+1) = sum(weight.*r)-targetR;
F(NumAsset+2) = sum(weight)-1;
end
This is an example from financial mathematics and Biao explains it in more detail in a post over at his blog, mathfinance.cn. Now, it isn’t particularly computationally challenging since it only takes 6.5 seconds to run on my 2Ghz dual core laptop. It is, however, significantly more challenging than the toy problem I discussed in my original fsolve post. So, let’s see how much we can optimise it using NAG and any other techniques that come to mind.
Before going on, I’d just like to point out that we intentionally set the seed of the random number generator with
RandStream.setDefaultStream (RandStream('mt19937ar','seed',1));
to ensure we are always operating with the same data set. This is purely for benchmarking purposes.
Optimisation trick 1 – replacing fsolve with NAG’s c05nb
The first thing I had to do to Biao’s code in order to apply the NAG toolbox was to split it into two files. We have the main program, fsolve_markowitz_NAG.m
function MarkowitzWeight = fsolve_markowitz_NAG()
global r targetR rCOV;
%seed random generator to ensure same results every time for benchmark purposes
RandStream.setDefaultStream (RandStream('mt19937ar','seed',1));
% simulate 500 stocks return
SimR = randn(1000,500);
r = mean(SimR)'; % use mean return as expected return
targetR = 0.02;
rCOV = cov(SimR); % covariance matrix
NumAsset = length(r);
startX = [1/NumAsset*ones(1,NumAsset), 1, 1];
tic
x = c05nb('fsolve_obj_NAG',startX);
toc
MarkowitzWeight = x(1:NumAsset);
end
and the objective function, fsolve_obj_NAG.m
function [F,iflag] = fsolve_obj_NAG(n,x,iflag)
global r targetR rCOV;
NumAsset = length(r);
F = zeros(1,NumAsset+2);
weight = x(1:NumAsset); % for asset weights
lambda = x(NumAsset+1);
mu = x(NumAsset+2);
for i = 1:NumAsset
F(i) = weight(i)*sum(rCOV(i,:))-lambda*r(i)-mu;
end
F(NumAsset+1) = sum(weight.*r)-targetR;
F(NumAsset+2) = sum(weight)-1;
end
I had to put the objective function into its own .m file because because the NAG toolbox currently doesn’t accept function handles (This may change in a future release I am reliably told). This is a pain but not a show stopper.
Note also that the function header for the NAG version of the objective function is different from the pure MATLAB version as
per my original article.
Transposition problems
The next thing to notice is that I have done the following in the main program, fsolve_markowitz_NAG.m
r = mean(SimR)';
compared to the original
r = mean(SimR);
This is because the NAG routine, c05nb, does something rather bizarre. I discovered that if you pass a 1xN matrix to NAGs c05nb then it gets transposed in the objective function to Nx1. Since Biao relies on this being 1xN when he does
F(NumAsset+1) = sum(weight.*r)-targetR;
we get an error unless you take the transpose of r in the main program. I consider this to be a bug in the NAG Toolbox and it is currently with NAG technical support.
Global variables
Sadly, there is no easy way to pass extra variables to the objective function when using NAG’s c05nb. In MATLAB Biao could do this
x = fsolve(@fsolve_markowitz,startX,options, r, targetR, rCOV);
No such luck with c05nb. The only way to get around it is to use global variables (Well, a small lie, there is another way, you can use reverse communication in a different NAG function, c05nd, but that’s a bit more complicated and I’ll leave it for another time I think)
So, It’s pretty clear that the NAG function isn’t as easy to use as MATLAB’s fsolve function but is it any faster? The following is typical.
>> tic;fsolve_markowitz_NAG;toc Elapsed time is 2.324291 seconds.
So, we have sped up our overall computation time by a factor of 3. Not bad, but nowhere near the 18 times speed-up that I demonstrated in my original post.
Optimisation trick 2 – Don’t sum so much
In his recent blog post, Biao challenged me to make his code almost 20 times faster and after applying my NAG Toolbox trick I had ‘only’ managed to make it 3 times faster. So, in order to see what else I might be able to do for him I ran his code through the MATLAB profiler and discovered that it spent the vast majority of its time in the following section of the objective function
for i = 1:NumAsset
F(i) = weight(i)*sum(rCOV(i,:))-lambda*r(i)-mu;
end
It seemed to me that the original code was calculating the sum of rCOV too many times. On a small number of assets (50 say) you’ll probably not notice it but with 500 assets, as we have here, it’s very wasteful.
So, I changed the above to
for i = 1:NumAsset
F(i) = weight(i)*sumrCOV(i)-lambda*r(i)-mu;
end
So,instead of rCOV, the objective function needs to be passed the following in the main program
sumrCOV=sum(rCOV)
We do this summation once and once only and make a big time saving. This is done in the files fsolve_markowitz_NAGnew.m and fsolve_obj_NAGnew.m
With this optimisation, along with using NAG’s c05nb we now get the calculation time down to
>> tic;fsolve_markowitz_NAGnew;toc Elapsed time is 0.203243 seconds.
Compared to the 6.5 seconds of the original code, this represents a speed-up of over 32 times. More than enough to satisfy Biao’s challenge.
Checking the answers
Let’s make sure that the results agree with each other. I don’t expect them to be exactly equal due to round off errors etc but they should be extremely close. I check that the difference between each result is less than 1e-7:
original_results = fsolve_markowitz_MATLAB;
nagver1_results = fsolve_markowitz_NAGnew;
>> all(abs(original_results - nagver1_results)<1e8)
ans =
1
That’ll do for me!
Summary
The current iteration of the NAG Toolbox for MATLAB (Mark 22) may not be as easy to use as native MATLAB toolbox functions (for this example at least) but it can often provide useful speed-ups and in this example, NAG gave us a factor of 3 improvement compared to using fsolve.
For this particular example, however, the more impressive speed-up came from pushing the code through the MATLAB profiler, identifying the hotspot and then doing something about it. There are almost certainly more optimisations to make but with the code running at less than a quarter of a second on my modest little laptop I think we will leave it there for now.