Walking Randomly

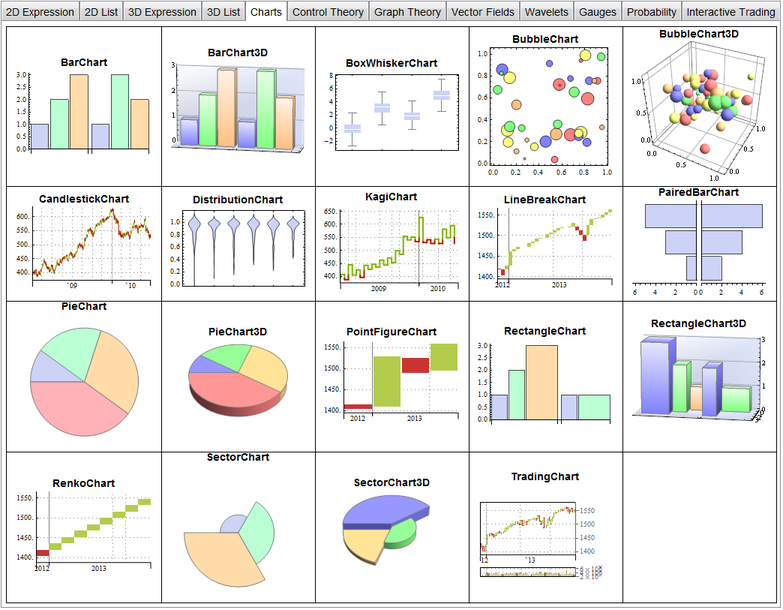
I’m working on a presentation involving Mathematica 9 at the moment and found myself wanting a gallery of all built-in plots using default settings.  Since I couldn’t find such a gallery, I made one myself.  The notebook is available here and includes 99 built-in plots, charts and gauges generated using default settings.  If you hover your mouse over one the plots in the Mathematica notebook, it will display a ToolTip showing usage notes for the function that generated it.

The gallery only includes functions that are fully integrated with Mathematica so doesn’t include things from add-on packages such as StatisticalPlots.

A screenshot of the gallery is below.  I haven’t made an in-browser interactive version due to size.

Google Reader has been a part of my life for several years now, forming the basis of my news reading habits.  Barely a day goes by that I don’t use it via my Android phone, iPad or the web and I have dozens of feeds effortlessly synced across all platforms.  It is, along with Dropbox, one of the most useful cloud services I have signed up for…and now its gone.

I guess I shouldn’t complain too much–after all it is a free service just like Twitter, Facebook, Evernote, Dropbox, Gmail, etc and so Google has every right to yank it away from me if that’s what they want to do.  What the cloud giveth, the cloud taketh away and all that.

What if your favourite cloud-based service was switched off?

This has led me to face up to something I’ve always had at the back of my mind but, until now, never really worried about too much– I rely far too much on services that are potentially ephemeral and I have no control over.  The loss of Google Reader from my life is frustrating but hardly the end of the world.  The loss of something like Dropbox, Evernote, Facebook or Gmail would cause me a lot more pain.

The data I upload to these services may be mine but the platforms are not and since I don’t pay a penny for any of them (Dropbox being a major exception) I am not sure what my legal rights may be.  If, for example, a company such as Evernote were to suddenly say ‘This free-access stuff isn’t working out for us so we deleted all your stuff and closed your account, thanks for playing.’, would I have any legal recourse?  Even more importantly, would I have a local backup?

Longevity and owning your own platform.

Another issue to consider is longevity.  Over the years I have invested time and money in dozens of software applications and, apart from a few notable exceptions where the licensing was crazy, I can still run any one of them today.  Languishing in the depths of my hard drives are files so old that they can only be read by ancient applications written by long-dead software development companies yet I can still launch the application and access the data.  I can do this because I physically own the platform.  The only way someone could prevent me from using the software and data on this platform is to physically take it from me.

To prevent me from using a cloud based service, however, it seems that all it takes is for that service to become unpopular.

Ever since I took a look at GPU accelerating simple Monte Carlo Simulations using MATLAB, I’ve been disappointed with the performance of its GPU random number generator. In MATLAB 2012a, for example, it’s not much faster than the CPU implementation on my GPU hardware.  Consider the following code

function gpuRandTest2012a(n)

mydev=gpuDevice();
disp('CPU - Mersenne Twister');
tic
CPU = rand(n);
toc

sg = parallel.gpu.RandStream('mrg32k3a','Seed',1);
parallel.gpu.RandStream.setGlobalStream(sg);
disp('GPU - mrg32k3a');
tic
Rg = parallel.gpu.GPUArray.rand(n);
wait(mydev);
toc

Running this on MATLAB 2012a on my laptop gives me the following typical times (If you try this out yourself, the first run will always be slower for various reasons I’ll not go into here)

>> gpuRandTest2012a(10000)
CPU - Mersenne Twister
Elapsed time is 1.330505 seconds.
GPU - mrg32k3a
Elapsed time is 1.006842 seconds.

Running the same code on MATLAB 2012b, however, gives a very pleasant surprise with typical run times looking like this

CPU - Mersenne Twister
Elapsed time is 1.590764 seconds.
GPU - mrg32k3a
Elapsed time is 0.185686 seconds.

So, generation of random numbers using the GPU is now over 7 times faster than CPU generation on my laptop hardware–a significant improvment on the previous implementation.

New generators in 2012b

The MATLAB developers went a little further in 2012b though.  Not only have they significantly improved performance of the mrg32k3a combined multiple recursive generator, they have also implemented two new GPU random number generators based on the Random123 library.  Here are the timings for the generation of 100 million random numbers in MATLAB 2012b

• Get the code – gpuRandTest2012b.m

CPU - Mersenne Twister
Elapsed time is 1.370252 seconds.
GPU - mrg32k3a
Elapsed time is 0.186152 seconds.
GPU - Threefry4x64-20
Elapsed time is 0.145144 seconds.
GPU - Philox4x32-10
Elapsed time is 0.129030 seconds.

Bear in mind that I am running this on the relatively weak GPU of my laptop!  If anyone runs it on something stronger, I’d love to hear of your results.

• Laptop model: Dell XPS L702X
• CPU: Intel Core i7-2630QM @2Ghz software overclockable to 2.9Ghz. 4 physical cores but total 8 virtual cores due to Hyperthreading.
• GPU: GeForce GT 555M with 144 CUDA Cores.  Graphics clock: 590Mhz.  Processor Clock:1180 Mhz. 3072 Mb DDR3 Memeory
• RAM: 8 Gb
• OS: Windows 7 Home Premium 64 bit.
• MATLAB: 2012a/2012b

Welcome to the latest Month of Math Software here at WalkingRandomly.  If you have any mathematical software news or blogposts that you’d like to share with a larger audience, feel free to contact me.  Thanks to everyone who contributed news items this month, I couldn’t do it without you.

The NAG Library for Java

• The Numerical Algorithms Group (NAG) have been producing numerical libraries for over 40 years and now they have one for Java.

MATLAB-a-likes

• Version 3.6.4 of Octave, the free, open-source MATLAB clone has been released.  This version contains some minor bug fixes.  To see everything that’s new since version 3.6, take a look at the NEWS file.  If you like MATLAB syntax but don’t like the price, Octave may well be for you.
• The frequently updated Euler Math Toolbox is now at version 20.98 with a full list of changes in the log.  Scanning through the recent changes log, I came across the very nice iteratefunction which works as follows

  >iterate("cos(x)",1,100,till="abs(cos(x)-x)<0.001")
  
  [ 1  0.540302305868  0.857553215846  0.654289790498  0.793480358743
  0.701368773623  0.763959682901  0.722102425027  0.750417761764
  0.731404042423  0.744237354901  0.735604740436  0.74142508661
  0.737506890513  0.740147335568  0.738369204122  0.739567202212 ]

Mathematical and Scientific Python

• The Python based computer algebra system, SAGE, has been updated to version 5.7.  The full list of changes is at http://www.sagemath.org/mirror/src/changelogs/sage-5.7.txt
• Numpy is the fundamental Python package required for numerical computing with Python.  Numpy is now at version 1.7 and you can see what’s new by taking a look at the release notes

Spreadsheet news

• A new version of Microsoft Excel, the 800 pound gorilla of the spreadsheet world, was actually released back in January as part of Office 2013 but I managed to miss it somehow.  An overview of what’s new in Excel 2013 is available in a blog post from Microsoft, along with a list of new functions in Excel 2013 and a note warning of the possibility of calculation differences between ‘normal’ PCs and those running Windows RT.  More in-depth articles include My first Excel 2013 chart, Excel 2013 in depth, Introduction to PowerPivot in Excel 2013 and the new ISFORUMULA Function in 2013.
• Hot on the heels of Microsoft’s product is a new version of the superb, completely free LibreOffice.  Version 4.0 was released on 7 February 2013 and includes a wide range of new features.  My favourite new feature, by far, is the inclusion of a Logo interpreter!  LibreLogo is ‘A Logo-Python programming environment with interactive turtle vector graphics for education and desktop publishing‘  and there are some blog posts about it here and here.  Another improvement I want to point out is the fact that the random number function in Libre Office Calc has been significantly improved.

R and stuff

• A new version of R, the open source standard for statistical computing, has been released.  Version 2.15.3 is probably going to be the last release before version 3 comes out.  The full list of changes can be found at http://cran.r-project.org/bin/windows/base/NEWS.R-2.15.3.html
• Version 0.4.0 of Shiny has been released and the Shiny tutorial has been updated.

This and that

• The commercial computer algebra system, Magma, has seen another incremental update in version 2.19-3.
• The NCAR Command Language was updated to version 6.1.2.
• IDL was updated to version 8.2.2.  Since I’m currenty obsessed with random number generators, I’ll point out that in this release IDL finally moves away from an old Numerical Recipies generator and now uses the Mersenne Twister like almost everybody else.

From the blogs

• The guys at AccelerEyes have been benchmarking NVIDIA’s new Tesla K20.
• NAG’s David Sayers asks  ‘Would you like the NAG Routines in Different Precisions?’
• Wolfram Research celebrates the Centennial of Markov Chains.
• Stephen Wolfram asks ‘What Should we call the language of Mathematica?’
• A couple of bloggers discuss performing Monte Carlo simulations using javascript (here and here).  I say ‘Fine, but be careful because the Javascript random number generators are not too good’

In a recent article, Matt Asher considered the feasibility of doing statistical computations in JavaScript.  In particular, he showed that the generation of 10 million normal variates can be as fast in Javascript as it is in R provided you use Google’s Chrome for the web browser.  From this, one might infer that using javascript to do your Monte Carlo simulations could be a good idea.

It is worth bearing in mind, however, that we are not comparing like for like here.

The default random number generator for R uses the Mersenne Twister algorithm which is of very high quality, has a huge period and is well suited for Monte Carlo simulations.  It is also the default algorithm for modern versions of MATLAB and is available in many other high quality mathematical products such as Mathematica, The NAG library, Julia and Numpy.

The algorithm used for Javascript’s math.random() function depends upon your web-browser.  A little googling uncovered a document that gives details on some implementations.  According to this document, Internet Explorer and Firefox both use 48 bit Linear Congruential Generator (LCG)-style generators but use different methods to set the seed.  Safari on Mac OS X uses a 31 bit LCG generator and Version 8 of Chrome on Windows uses 2 calls to rand() in msvcrt.dll.  So, for V8 Chrome on Windows, Math.random() is a floating point number consisting of the second rand() value, concatenated with the first rand() value, divided by 2^30.

The points I want to make here are:-

• Javascript’s math.random() uses different algorithms between browsers.
• These algorithms have relatively small periods.  For example, a 48-bit LCG has a period of 2^48 compared to 2^19937-1 for Mersenne Twister.
• They have poor statistical properties.  For example, the 48bit LCG implemented in Java’s java.util.Random function fails 21 of the BigCrush tests.  I haven’t found any test results for JavaScript implementations but expect them to be at least as bad. I understand that Mersenne Twister fails 2 of the BigCrush tests but these are not considered to be an issue by many people.
• You can’t manually set the seed for math.random() so reproducibility is impossible.