Archive for January, 2013
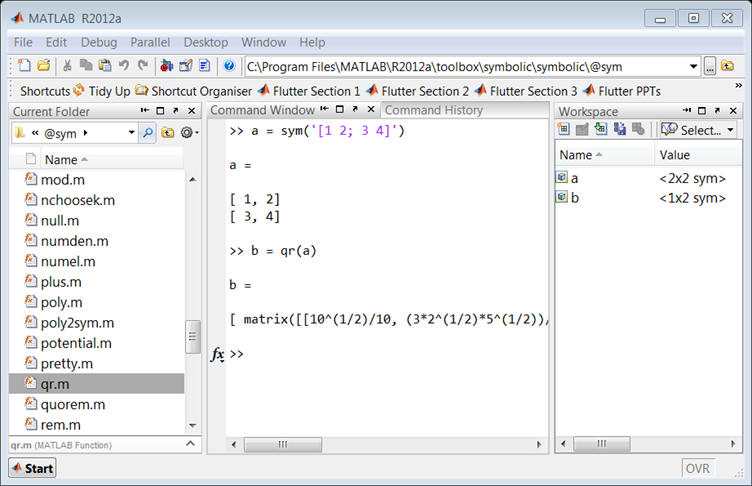
In a recent blog post, I demonstrated how to use the MATLAB 2012a Symbolic Toolbox to perform Variable precision QR decomposition in MATLAB. The result was a function called vpa_qr which did the necessary work.
>> a=vpa([2 1 3;-1 0 7; 0 -1 -1]); >> [Q R]=vpa_qr(a);
I’ve suppressed the output because it’s so large but it definitely works. When I triumphantly presented this function to the user who requested it he was almost completely happy. What he really wanted, however, was for this to work:
>> a=vpa([2 1 3;-1 0 7; 0 -1 -1]); >> [Q R]=qr(a);
In other words he wants to override the qr function such that it accepts variable precision types. MATLAB 2012a does not allow this:
>> a=vpa([2 1 3;-1 0 7; 0 -1 -1]); >> [Q R]=qr(a) Undefined function 'qr' for input arguments of type 'sym'.
I put something together that did the job for him but felt that it was unsatisfactory. So, I sent my code to The MathWorks and asked them if what I had done was sensible and if there were any better options. A MathWorks engineer called Hugo Carr sent me such a great, detailed reply that I asked if I could write it up as a blog post. Here is the result:
Approach 1: Define a new qr function, with a different name (such as vpa_qr). This is probably the safest and simplest option and was the method I used in the original blog post.
- Pros: The new function will not interfere with your MATLAB namespace
- Cons: MATLAB will only use this function if you explicitly define that you wish to use it in a given function. You would have to find all prior references to the qr algorithm and make a decision about which to use.
Approach 2: Define a new qr function and use the ‘isa’ function to catch instances of ‘sym’. This is the approach I took in the code I sent to The MathWorks.
function varargout = qr( varargin )
if nargin == 1 && isa( varargin{1}, 'sym' )
[varargout{1:nargout}] = vpa_qr( varargin{:} );
else
[varargout{1:nargout}] = builtin( 'qr', varargin{:} );
end
- Pros: qr will always select the correct code when executed on sym objects
- Cons: This code only works for shadowing built-ins and will produce a warning reminding you of this fact. If you wish to extend this pattern for other class types, you’ll require a switch statement (or nested if-then-else block), which could lead to a complex comparison each time qr is invoked (and subsequent performance hit). Note that switch statements in conjunction with calls to ‘isa’ are usually indicators that an object oriented approach is a better way forward.
Approach 3: The MathWorks do not recommend that you modify your MATLAB install. However for completeness, it is possible to add a new ‘method’ to the sym class by dropping your function into the sym class folder. For MATLAB 2012a on Windows, this folder is at
C:\Program Files\MATLAB\R2012a\toolbox\symbolic\symbolic\@sym
For the sake of illustration, here is a simplified implementation. Call it qr.m
function result = qr( this ) result = feval(symengine,'linalg::factorQR', this); end
Pros: Functions saved to a class folder take precedence over built in functionality, which means that MATLAB will always use your qr method for sym objects.
Cons: If you share code which uses this functionality, it won’t run on someone’s computer unless they update their sym class folder with your qr code. Additionally, if a new method is added to a class it may shadow the behaviour of other MATLAB functionality and lead to unexpected behaviour in Symbolic Toolbox.
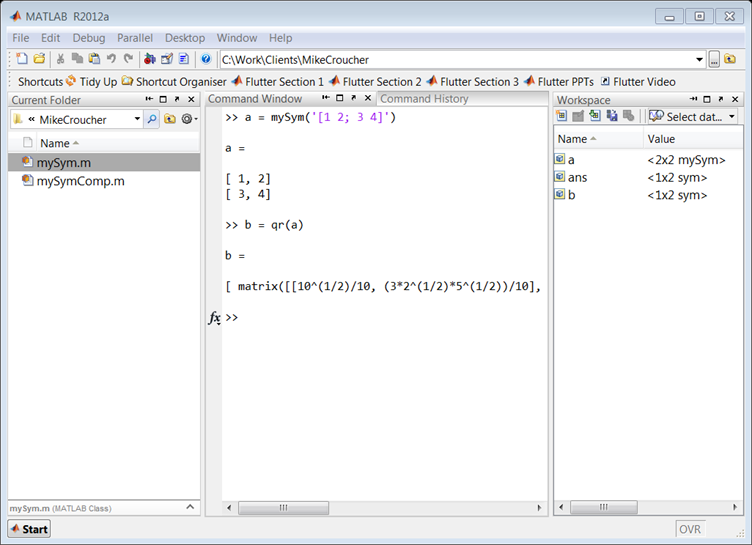
Approach 4: For more of an object-oriented approach it is possible to sub-class the sym class, and add a new qr method.
classdef mySym < sym
methods
function this = mySym(arg)
this = this@sym(arg);
end
function result = qr( this )
result = feval(symengine,'linalg::factorQR', this);
end
end
end
Pros: Your change can be shipped with your code and it will work on a client’s computer without having to change the sym class.
Cons: When calling superclass methods on your mySym objects (such as sin(mySym1)), the result will be returned as the superclass unless you explicitly redefine the method to return the subclass.
N.B. There is a lot of literature which discusses why inheritance (subclassing) to augment a class’s behaviour is a bad idea. For example, if Symbolic Toolbox developers decide to add their own qr method to the sym API, overriding that function with your own code could break the system. You would need to update your subclass every time the superclass is updated. This violates encapsulation, as the subclass implementation depends on the superclass. You can avoid problems like these by using composition instead of inheritance.
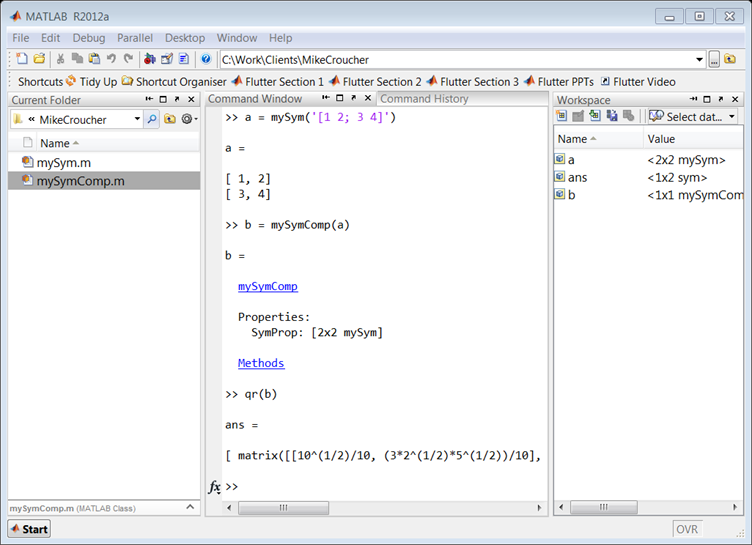
Approach 5: You can create a new sym class by using composition, but it takes a little longer than the other approaches. Essentially, this involves creating a wrapper which provides the functionality of the original class, as well as any new functions you are interested in.
classdef mySymComp
properties
SymProp
end
methods
function this = mySymComp(symInput)
this.SymProp = symInput;
end
function result = qr( this )
result = feval(symengine,'linalg::factorQR', this.SymProp);
end
end
end
Note that in this example we did not add any of the original sym functions to the mySymComp class, however this can be done for as many as you like. For example, I might like to use the sin method from the original sym class, so I can just delegate to the methods of the sym object that I passed in during construction:
classdef mySymComp
properties
SymProp
end
methods
function this = mySymComp(symInput)
this.SymProp = symInput;
end
function result = qr( this )
result = feval(symengine,'linalg::factorQR', this.SymProp);
end
function G = sin(this)
G = mySymComp(sin(this.SymProp));
end
end
end
Pros: The change is totally encapsulated, and cannot be broken save for a significant change to the sym api (for example, the MathWorks adding a qr method to sym would not break your code).
Cons: The wrapper can be time consuming to write, and the resulting object is not a ‘sym’, meaning that if you pass a mySymComp object ‘a’ into the following code:
isa(a, 'sym')
MATLAB will return ‘false’ by default.
I am having a friendly argument with a colleague over how you calculate the peak number of floating operations per second (flops) for devices that support Fused Multiply Add (FMA). The FMA operation is d=a+b*c, an operation that can be done in one cycle on devices that support it.
I say that an FMA operation is two flops, he says it’s one. So, when I calculate the theoretical peak of a device I get twice the value he does. So, what do you think..is FMA one flop or two?
I like the StackOverflow range of question and answer sites and have hopped on and off them almost since the very beginning. When I logged in recently I was informed that one of my questions had been awarded the ‘Famous Question’ badge..i.e. it had been viewed over 10,000 times. The relevant question was Python blogs that you regularly follow? which was asked by me in the very early days of the site. Not only has it received 63 community up-votes and over 10,000 views but it’s also been closed as ‘Not constructive’ by senior members of the Stack Overflow community.
I find this contrast amusing!
In a recent article, Citing software in research papers, I discussed how to cite various software packages. One of the commentators suggested that I should contact The Mathworks if I wanted to know how to cite MATLAB. I did this and asked for permission to blog the result. This is what they suggested:
To cite MATLAB (and in this case a toolbox) you can use this:
MATLAB and Statistics Toolbox Release 2012b, The MathWorks, Inc., Natick, Massachusetts, United States.
This is the format prescribed by both the Chicago Manual of Style and the Microsoft Manual of Style. If you use a different style guide, you may apply a different format, but should observe the capitalization shown above, and include the appropriate release number. If the MathWorks release number (in the format YYYYa or YYYYb) is not readily available, you can use the point release numbers for the software, as in:
MATLAB 8.0 and Statistics Toolbox 8.1, The MathWorks, Inc., Natick, Massachusetts, United States.
Thanks to The Mathworks for allowing me to reproduce this communication here at WalkingRandomly.
R has a citation() command that recommends how to cite the use of R in your publications, information that is also included in R’s Frequently Asked Questions document.
To cite R in publications use:
R Core Team (2012). R: A language and environment for
statistical computing. R Foundation for Statistical
Computing, Vienna, Austria. ISBN 3-900051-07-0, URL
http://www.R-project.org/.
A BibTeX entry for LaTeX users is
@Manual{,
title = {R: A Language and Environment for Statistical Computing},
author = {{R Core Team}},
organization = {R Foundation for Statistical Computing},
address = {Vienna, Austria},
year = {2012},
note = {{ISBN} 3-900051-07-0},
url = {http://www.R-project.org/},
}
We have invested a lot of time and effort in creating R, please
cite it when using it for data analysis. See also
‘citation("pkgname")’ for citing R packages
This led me to wonder how often people cite the software they use. For example, if you publish the results of a simulation written in MATLAB do you cite MATLAB in any way? How about if you used Origin or Excel to produce a curve fit, would you cite that? Would you cite your plotting software, numerical libraries or even compiler?
The software sustainability institute (SSI), of which I recently became a fellow, has guidelines on how to cite software.
The Numerical Algorithms Group (NAG) are principally known for their numerical library but they also offer products such as a MATLAB toolbox and a Fortran compiler. My employer, The University of Manchester, has a full site license for most of NAG’s stuff where it is heavily used by both our students and researchers.
While at a recent software conference, I saw a talk by NAG’s David Sayers where he demonstrated some of the features of the NAG Fortran Compiler. During this talk he showed some examples of broken Fortran and asked us if we could spot how they were broken without compiler assistance. I enjoyed the talk and so asked David if he would mind writing a guest blog post on the subject for WalkingRandomly. He duly obliged.
This is a guest blog post by David Sayers of NAG.
What do you want from your Fortran compiler? Some people ask for extra (non-standard) features, others require very fast execution speed. The very latest extensions to the Fortran language appeal to those who like to be up to date with their code.
I suspect that very few would put enforcement of the Fortran standard at the top of their list, yet this essential if problems are to be avoided in the future. Code written specifically for one compiler is unlikely to work when computers change, or may contain errors that appear only intermittently. Without access to at least one good checking compiler, the developer or support desk will be lacking a valuable tool in the fight against faulty code.
The NAG Fortran compiler is such a tool. It is used extensively by NAG’s own staff to validate their library code and to answer user-support queries involving user’s Fortran programs. It is available on Windows, where it has its own IDE called Fortran Builder, and on Unix platforms and Mac OS X.
Windows users also have the benefit of some Fortran Tools bundled in to the IDE. Particularly nice is the Fortran polisher which tidies up the presentation of your source files according to user-specified preferences.
The compiler includes most Fortran 2003 features, very many Fortran 2008 features and the most commonly used features of OpenMP 3.0 are supported.
The principal developer of the compiler is Malcolm Cohen, co-author of the book, Modern Fortran Explained
Of all people Malcolm Cohen should know Fortran and the way the standard should be enforced!
His compiler reflects that knowledge and is designed to assist the programmer to detect how programs might be faulty due to a departure from the Fortran standard or prone to trigger a run time error. In either case the diagnostics of produced by the compiler are clear and helpful and can save the developer many hours of laborious bug-tracing. Here are some particularly simple examples of faulty programs. See if you can spot the mistakes, and think how difficult these might be to detect in programs that may be thousands of times longer:
Example 1
Program test
Real, Pointer :: x(:, :)
Call make_dangle
x(10, 10) = 0
Contains
Subroutine make_dangle
Real, Target :: y(100, 200)
x => y
End Subroutine make_dangle
End Program test
Example 2
Program dangle2 Real,Pointer :: x(:),y(:) Allocate(x(100)) y => x Deallocate(x) y = 3 End
Example 3
program more
integer n, i
real r, s
equivalence (n,r)
i=3
r=2.5
i=n*n
write(6,900) i, r
900 format(' i = ', i5, ' r = ', f10.4)
stop 'ok'
end
Example 4
program trouble1
integer n
parameter (n=11)
integer iarray(n)
integer i
do 10 i=1,10
iarray(i) = i
10 continue
write(6,900) iarray
900 format(' iarray = ',11i5)
stop 'ok'
end
And finally if this is all too easy …
Example 5
! E04UCA Example Program Text
! Mark 23 Release. NAG Copyright 2011.
MODULE e04ucae_mod
! E04UCA Example Program Module:
! Parameters and User-defined Routines
! .. Use Statements ..
USE nag_library, ONLY : nag_wp
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Parameters ..
REAL (KIND=nag_wp), PARAMETER :: one = 1.0_nag_wp
REAL (KIND=nag_wp), PARAMETER :: zero = 0.0_nag_wp
INTEGER, PARAMETER :: inc1 = 1, lcwsav = 1, &
liwsav = 610, llwsav = 120, &
lrwsav = 475, nin = 5, nout = 6
CONTAINS
SUBROUTINE objfun(mode,n,x,objf,objgrd,nstate,iuser,ruser)
! Routine to evaluate objective function and its 1st derivatives.
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
REAL (KIND=nag_wp), INTENT (OUT) :: objf
INTEGER, INTENT (INOUT) :: mode
INTEGER, INTENT (IN) :: n, nstate
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (INOUT) :: objgrd(n), ruser(*)
REAL (KIND=nag_wp), INTENT (IN) :: x(n)
INTEGER, INTENT (INOUT) :: iuser(*)
! .. Executable Statements ..
IF (mode==0 .OR. mode==2) THEN
objf = x(1)*x(4)*(x(1)+x(2)+x(3)) + x(3)
END IF
IF (mode==1 .OR. mode==2) THEN
objgrd(1) = x(4)*(x(1)+x(1)+x(2)+x(3))
objgrd(2) = x(1)*x(4)
objgrd(3) = x(1)*x(4) + one
objgrd(4) = x(1)*(x(1)+x(2)+x(3))
END IF
RETURN
END SUBROUTINE objfun
SUBROUTINE confun(mode,ncnln,n,ldcj,needc,x,c,cjac,nstate,iuser,ruser)
! Routine to evaluate the nonlinear constraints and their 1st
! derivatives.
! .. Implicit None Statement ..
IMPLICIT NONE
! .. Scalar Arguments ..
INTEGER, INTENT (IN) :: ldcj, n, ncnln, nstate
INTEGER, INTENT (INOUT) :: mode
! .. Array Arguments ..
REAL (KIND=nag_wp), INTENT (OUT) :: c(ncnln)
REAL (KIND=nag_wp), INTENT (INOUT) :: cjac(ldcj,n), ruser(*)
REAL (KIND=nag_wp), INTENT (IN) :: x(n)
INTEGER, INTENT (INOUT) :: iuser(*)
INTEGER, INTENT (IN) :: needc(ncnln)
! .. Executable Statements ..
IF (nstate==1) THEN
! First call to CONFUN. Set all Jacobian elements to zero.
! Note that this will only work when 'Derivative Level = 3'
! (the default; see Section 11.2).
cjac(1:ncnln,1:n) = zero
END IF
IF (needc(1)>0) THEN
IF (mode==0 .OR. mode==2) THEN
c(1) = x(1)**2 + x(2)**2 + x(3)**2 + x(4)**2
END IF
IF (mode==1 .OR. mode==2) THEN
cjac(1,1) = x(1) + x(1)
cjac(1,2) = x(2) + x(2)
cjac(1,3) = x(3) + x(3)
cjac(1,4) = x(4) + x(4)
END IF
END IF
IF (needc(2)>0) THEN
IF (mode==0 .OR. mode==2) THEN
c(2) = x(1)*x(2)*x(3)*x(4)
END IF
IF (mode==1 .OR. mode==2) THEN
cjac(2,1) = x(2)*x(3)*x(4)
cjac(2,2) = x(1)*x(3)*x(4)
cjac(2,3) = x(1)*x(2)*x(4)
cjac(2,4) = x(1)*x(2)*x(3)
END IF
END IF
RETURN
END SUBROUTINE confun
END MODULE e04ucae_mod
PROGRAM e04ucae
! E04UCA Example Main Program
! .. Use Statements ..
USE nag_library, ONLY : dgemv, e04uca, e04wbf, nag_wp
USE e04ucae_mod, ONLY : confun, inc1, lcwsav, liwsav, llwsav, lrwsav, &
nin, nout, objfun, one, zero
! .. Implicit None Statement ..
! IMPLICIT NONE
! .. Local Scalars ..
! REAL (KIND=nag_wp) :: objf
INTEGER :: i, ifail, iter, j, lda, ldcj, &
ldr, liwork, lwork, n, nclin, &
ncnln, sda, sdcjac
! .. Local Arrays ..
REAL (KIND=nag_wp), ALLOCATABLE :: a(:,:), bl(:), bu(:), c(:), &
cjac(:,:), clamda(:), objgrd(:), &
r(:,:), work(:), x(:)
REAL (KIND=nag_wp) :: ruser(1), rwsav(lrwsav)
INTEGER, ALLOCATABLE :: istate(:), iwork(:)
INTEGER :: iuser(1), iwsav(liwsav)
LOGICAL :: lwsav(llwsav)
CHARACTER (80) :: cwsav(lcwsav)
! .. Intrinsic Functions ..
INTRINSIC max
! .. Executable Statements ..
WRITE (nout,*) 'E04UCA Example Program Results'
! Skip heading in data file
READ (nin,*)
READ (nin,*) n, nclin, ncnln
liwork = 3*n + nclin + 2*ncnln
lda = max(1,nclin)
IF (nclin>0) THEN
sda = n
ELSE
sda = 1
END IF
ldcj = max(1,ncnln)
IF (ncnln>0) THEN
sdcjac = n
ELSE
sdcjac = 1
END IF
ldr = n
IF (ncnln==0 .AND. nclin>0) THEN
lwork = 2*n**2 + 20*n + 11*nclin
ELSE IF (ncnln>0 .AND. nclin>=0) THEN
lwork = 2*n**2 + n*nclin + 2*n*ncnln + 20*n + 11*nclin + 21*ncnln
ELSE
lwork = 20*n
END IF
ALLOCATE (istate(n+nclin+ncnln),iwork(liwork),a(lda,sda), &
bl(n+nclin+ncnln),bu(n+nclin+ncnln),c(max(1, &
ncnln)),cjac(ldcj,sdcjac),clamda(n+nclin+ncnln),objgrd(n),r(ldr,n), &
x(n),work(lwork))
IF (nclin>0) THEN
READ (nin,*) (a(i,1:sda),i=1,nclin)
END IF
READ (nin,*) bl(1:(n+nclin+ncnln))
READ (nin,*) bu(1:(n+nclin+ncnln))
READ (nin,*) x(1:n)
! Initialise E04UCA
ifail = 0
CALL e04wbf('E04UCA',cwsav,lcwsav,lwsav,llwsav,iwsav,liwsav,rwsav, &
lrwsav,ifail)
! Solve the problem
ifail = -1
CALL e04uca(n,nclin,ncnln,lda,ldcj,ldr,a,bl,bu,confun,objfun,iter, &
istate,c,cjac,clamda,objf,objgrd,r,x,iwork,liwork,work,lwork,iuser, &
ruser,lwsav,iwsav,rwsav,ifail)
SELECT CASE (ifail)
CASE (0:6,8)
WRITE (nout,*)
WRITE (nout,99999)
WRITE (nout,*)
DO i = 1, n
WRITE (nout,99998) i, istate(i), x(i), clamda(i)
END DO
IF (nclin>0) THEN
! A*x --> work.
! The NAG name equivalent of dgemv is f06paf
CALL dgemv('N',nclin,n,one,a,lda,x,inc1,zero,work,inc1)
WRITE (nout,*)
WRITE (nout,*)
WRITE (nout,99997)
WRITE (nout,*)
DO i = n + 1, n + nclin
j = i - n
WRITE (nout,99996) j, istate(i), work(j), clamda(i)
END DO
END IF
IF (ncnln>0) THEN
WRITE (nout,*)
WRITE (nout,*)
WRITE (nout,99995)
WRITE (nout,*)
DO i = n + nclin + 1, n + nclin + ncnln
j = i - n - nclin
WRITE (nout,99994) j, istate(i), c(j), clamda(i)
END DO
END IF
WRITE (nout,*)
WRITE (nout,*)
WRITE (nout,99993) objf
END SELECT
99999 FORMAT (1X,'Varbl',2X,'Istate',3X,'Value',9X,'Lagr Mult')
99998 FORMAT (1X,'V',2(1X,I3),4X,1P,G14.6,2X,1P,G12.4)
99997 FORMAT (1X,'L Con',2X,'Istate',3X,'Value',9X,'Lagr Mult')
99996 FORMAT (1X,'L',2(1X,I3),4X,1P,G14.6,2X,1P,G12.4)
99995 FORMAT (1X,'N Con',2X,'Istate',3X,'Value',9X,'Lagr Mult')
99994 FORMAT (1X,'N',2(1X,I3),4X,1P,G14.6,2X,1P,G12.4)
99993 FORMAT (1X,'Final objective value = ',1P,G15.7)
END PROGRAM e04ucae
Answers to this particular New Year quiz will be posted in a future blog post.
Welcome to the last 2012 edition of A Month of Math Software..slightly delayed thanks to the December festivities. Thanks to everyone who’s contributed news items over the last 2 years, please feel free to continue contacting me throughout 2013 and beyond.
AccelerEyes sells the MATLAB Jacket to The Mathworks
- AccelerEyes are the developers of GPU accelerated products such as Jacket for MATLAB and ArrayFire for C, C++, and Fortran. In a recent blog post, they announced that they have sold Jacket to The Mathworks. It will be interesting to see how The Mathworks integrate this technology into the Parallel Computing Toolbox (PCT) in the future. I sincerely hope that they don’t split the PCT into two products, one for GPUs and the other for CPUs!
Free computer algebra
- Maxima hit release 5.29-1 in December. Here’s the changelog.
- Sage version 5.5 has been released. Here’s the changelog.
- Euler is at version 20.
Numerical Libraries
- Version 5.3 of the ACML linear algebra library for AMD-based systems was released in December.
- Another of AMD’s libraries was updated this month. The Accelerated Parallel Processing (APP) SDK hit version 2.8 and includes a preview of AMD’s new C++ template library, Codename “Bolt.”. According to AMD, Bolt ‘makes it easier for developers to utilize the inherent performance and power efficiency benefits of heterogeneous computing’ The press release for this version of the APP SDK is available at http://developer.amd.com/wordpress/media/2012/10/APP-SDK-Bolt-CodeXL-Press-Release.pdf. Also, click here for more details concerning Bolt
- Numeric Javascript saw two releases, v1.2.5 and v1.2.6
- The HSL Software Library was updated this month adding three new routines to support Fredholm alternative for singular systems, efficient multiplication of the factors by a vector, and sparse forward solve.
- amgcl is an accelerated algebraic multigrid for C++. According to the software’s website ‘You can use amgcl to solve large sparse system of linear equations in three simple steps: first, you have to select method components (this is a compile time decision); second, the AMG hierarchy has to be constructed from a system matrix; and third, the hierarchy is used to solve the equation system for a given right-hand side’
Data Analysis and Visualisation
- GNU Data language is now at version 0.9.3. This is a ‘free, open source incremental compiler compatible with IDL and to some extent with PV-WAVE‘. There are some great screen shots on their website.
- DISLIN is at version 10.2.7. DISLIN is a high-level plotting library for C and Fortran.
- Version 0.10.0 of Pandas, The Python Data Analysis Library, was released in December 2012.
Maple IDE
- DigiArea have released an Eclipse based Integrated Development Environment (IDE) for Maple called, simply, Maple IDE. This commercial product is available for Linux, Windows and Mac OS X and seems to be a very similar concept to Wolfram’s Workbench for Mathematica.
Spreadsheets
- Gnumeric, a free spreadsheet program, is now at version 1.12.
- Version 3.6.4 of LibreOffice, the free office suite for multiple operating systems, was released this month. The release notes are at http://www.libreoffice.org/download/release-notes/. The spreadsheet component is called Calc and the list of features new to the 3.6.x branch can be found at http://www.libreoffice.org/download/3-6-new-features-and-fixes/
Commercial Number Theory
- MAGMA is now at version v2.19.2