Archive for the ‘Fractals’ Category
The MATLAB community site, MATLAB Central, is celebrating its 20th anniversary with a coding competition where the only aim is to make an interesting image with under 280 characters of code. The 280 character limit ensures that the resulting code is tweetable. There are a couple of things I really like about the format of this competition, other than the obvious fact that the only aim is to make something pretty!
- No MATLAB license is required! Sign up for a free MathWorks account and away you go. You can edit and run code in the browser.
Stealingreusing other people’s code is actively encouraged! The competition calls it remixing but GitHub users will recognize it as forking.
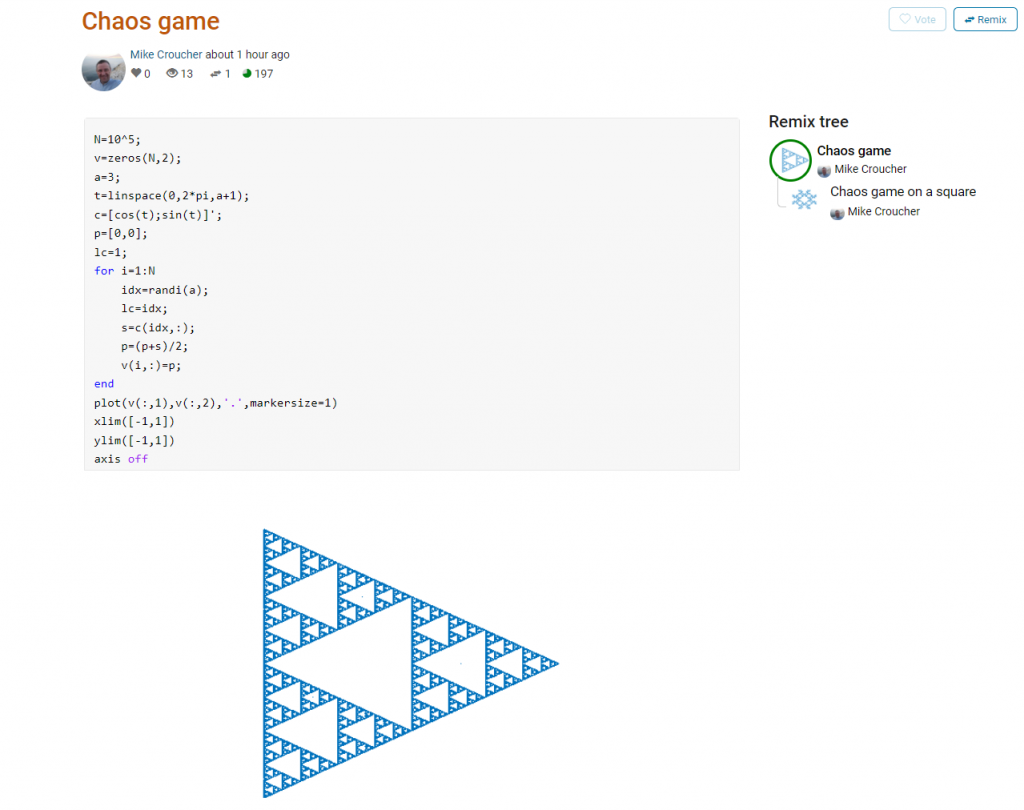
Here’s an example. I wrote a piece of code to render the Sierpiński triangle – Wikipedia using a simple random algorithm called the Chaos game.
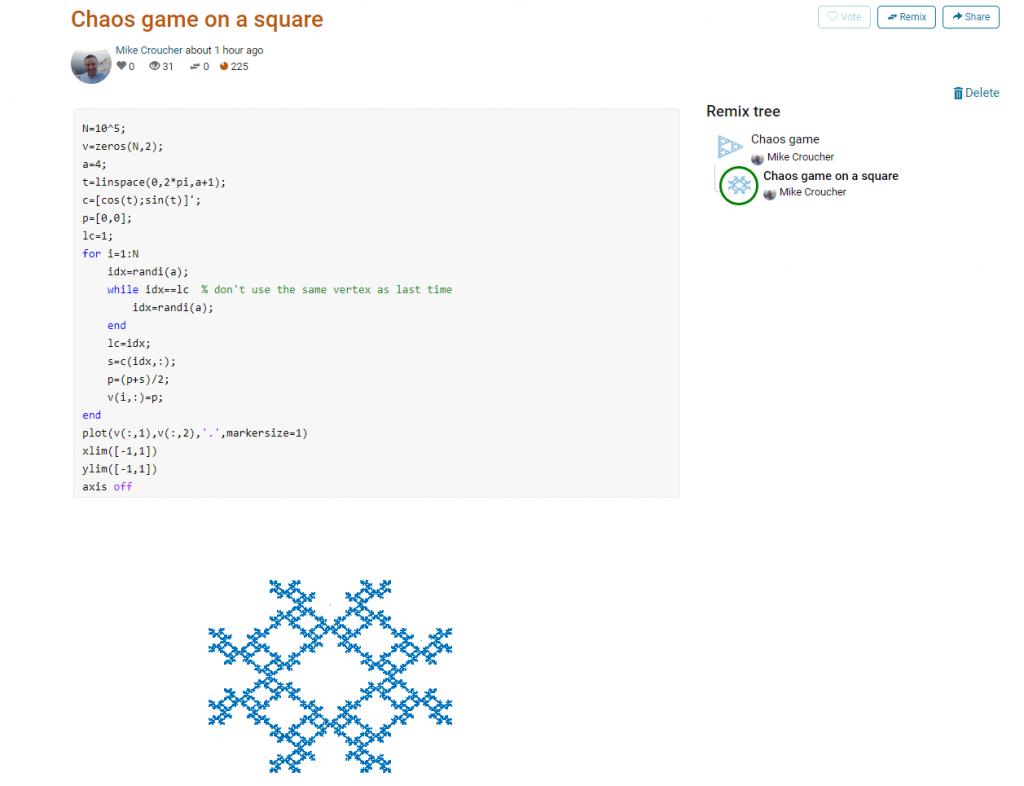
This is about as simple as the Chaos game gets and there are many things that could be done to produce a different image. As you can see from the Remix tree on the right hand side, I’ve already done one of them by changing a from 3 to 4 and adding some extra code to ensure that the same vertex doesn’t get chosen twice. This is result:
Someone else can now come along, hit the remix button and edit the code to produce something different again. Some things you might want to try for the chaos game include
- Try changing the value of a which is used in the variables t and c to produce the vertices of a polygon on an enclosing circle.
- Instead of just using the vertices of a polygon, try using the midpoints or another scheme for producing the attractor points completely.
- Try changing the scaling factor — currently p=(p+s)/2;
- Try putting limitations on which vertex is chosen. This remix ensures that the current vertex is different from the last one chosen.
- Each vertex is currently equally likely to be chosen using the code idx=randi(a); Think of ways to change the probabilities.
- Think of ways to colorize the plots.
Maybe the chaos game isn’t your thing. You are free to create your own design from scratch or perhaps you’d prefer to remix some of the other designs in the gallery.
The competition is just a few hours old and there are already some very nice ideas coming out.
In a recent blog-post, John Cook, considered when series such as the following converged for a given complex number z
z1 = sin(z)
z2 = sin(sin(z))
z3 = sin(sin(sin(z)))
John’s article discussed a theorem that answered the question for a few special cases and this got me thinking: What would the complete set of solutions look like? Since I was halfway through my commute to work and had nothing better to do, I thought I’d find out.
The following Mathematica code considers points in the square portion of the complex plane where both real and imaginary parts range from -8 to 8. If the sequence converges for a particular point, I colour it black.
LaunchKernels[4]; (*Set up for 4 core parallel compute*)
ParallelEvaluate[SetSystemOptions["CatchMachineUnderflow" -> False]];
convTest[z_, tol_, max_] := Module[{list},
list = Quiet[
NestWhileList[Sin[#] &, z, (Abs[#1 - #2] > tol &), 2, max]];
If[
Length[list] < max && NumericQ[list[[-1]]]
, 1, 0]
]
step = 0.005;
extent = 8;
AbsoluteTiming[
data = ParallelMap[convTest[#, 10*10^-4, 1000] &,
Table[x + I y, {y, -extent, extent, step}, {x, -extent, extent,
step}]
, {2}];]
ArrayPlot[data]

I quickly emailed John to tell him of my discovery but on actually getting to work I discovered that the above fractal is actually very well known. There’s even a colour version on Wolfram’s MathWorld site. Still, it was a fun discovery while it lasted
Other WalkingRandomly posts like this one:
Back in May 2009, just after Wolfram Alpha was released, I had a look to see which fractals had been implemented. Even at that very early stage there were a lot of very nice fractals that Wolfram Alpha could generate but I managed to come up with a list of fractals that Wolfram Alpha appeared to know about but couldn’t actually render.
On a whim I recently revisited that list and am very pleased to note that every single one of them has now been fully implemented! Very nice.
Can you find any Wolfram Alpha fractals that I missed in the original post?
Some time ago now, Sam Shah of Continuous Everywhere but Differentiable Nowhere fame discussed the standard method of obtaining the square root of the imaginary unit, i, and in the ensuing discussion thread someone asked the question “What is i^i – that is what is i to the power i?”
Sam immediately came back with the answer e^(-pi/2) = 0.207879…. which is one of the answers but as pointed out by one of his readers, Adam Glesser, this is just one of the infinite number of potential answers that all have the form e^{-(2k+1) pi/2} where k is an integer. Sam’s answer is the principle value of i^i (incidentally this is the value returned by google calculator if you google i^i – It is also the value returned by Mathematica and MATLAB). Life gets a lot more complicated when you move to the complex plane but it also gets a lot more interesting too.
While on the train into work one morning I was thinking about Sam’s blog post and wondered what the principal value of i^i^i (i to the power i to the power i) was equal to. Mathematica quickly provided the answer:
N[I^I^I] 0.947159+0.320764 I
So i is imaginary, i^i is real and i^i^i is imaginary again. Would i^i^i^i be real I wondered – would be fun if it was. Let’s see:
N[I^I^I^I] 0.0500922+0.602117 I
gah – a conjecture bites the dust – although if I am being honest it wasn’t a very good one. Still, since I have started making ‘power towers’ I may as well continue and see what I can see. Why am I calling them power towers? Well, the calculation above could be written as follows:
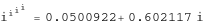
As I add more and more powers, the left hand side of the equation will tower up the page….Power Towers. We now have a sequence of the first four power towers of i:
i = i i^i = 0.207879 i^i^i = 0.947159 + 0.32076 I i^i^i^i = 0.0500922+0.602117 I
Sequences of power towers
“Will this sequence converge or diverge?”, I wondered. I wasn’t in the mood to think about a rigorous mathematical proof, I just wanted to play so I turned back to Mathematica. First things first, I needed to come up with a way of making an arbitrarily large power tower without having to do a lot of typing. Mathematica’s Nest function came to the rescue and the following function allows you to create a power tower of any size for any number, not just i.
tower[base_, size_] := Nest[N[(base^#)] &, base, size]
Now I can find the first term of my series by doing
In[1]:= tower[I, 0] Out[1]= I
Or the 5th term by doing
In[2]:= tower[I, 4] Out[2]= 0.387166 + 0.0305271 I
To investigate convergence I needed to create a table of these. Maybe the first 100 towers would do:
ColumnForm[
Table[tower[I, n], {n, 1, 100}]
]
The last few values given by the command above are
0.438272+ 0.360595 I 0.438287+ 0.360583 I 0.438287+ 0.3606 I 0.438275+ 0.360591 I 0.438289+ 0.360588 I
Now this is interesting – As I increased the size of the power tower, the result seemed to be converging to around 0.438 + 0.361 i. Further investigation confirms that the sequence of power towers of i converges to 0.438283+ 0.360592 i. If you were to ask me to guess what I thought would happen with large power towers like this then I would expect them to do one of three things – diverge to infinity, stay at 1 forever or quickly converge to 0 so this is unexpected behaviour (unexpected to me at least).
They converge, but how?
My next thought was ‘How does it converge to this value? In other words, ‘What path through the complex plane does this sequence of power towers take?” Time for a graph:
tower[base_, size_] := Nest[N[(base^#)] &, base, size];
complexSplit[x_] := {Re[x], Im[x]};
ListPlot[Map[complexSplit, Table[tower[I, n], {n, 0, 49, 1}]],
PlotRange -> All]
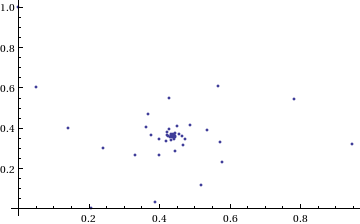
Who would have thought you could get a spiral from power towers? Very nice! So the next question is ‘What would happen if I took a different complex number as my starting point?’ For example – would power towers of (0.5 + i) converge?’
The answer turns out to be yes – power towers of (0.5 + I) converge to 0.541199+ 0.40681 I but the resulting spiral looks rather different from the one above.
tower[base_, size_] := Nest[N[(base^#)] &, base, size];
complexSplit[x_] := {Re[x], Im[x]};
ListPlot[Map[complexSplit, Table[tower[0.5 + I, n], {n, 0, 49, 1}]],
PlotRange -> All]
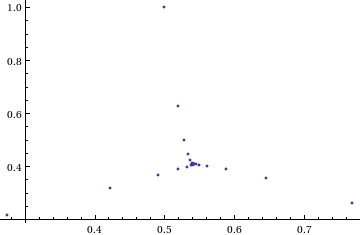 The zoo of power tower spirals
The zoo of power tower spirals
So, taking power towers of two different complex numbers results in two qualitatively different ‘convergence spirals’. I wondered how many different spiral types I might find if I consider the entire complex plane? I already have all of the machinery I need to perform such an investigation but investigation is much more fun if it is interactive. Time for a Manipulate
complexSplit[x_] := {Re[x], Im[x]};
tower[base_, size_] := Nest[N[(base^#)] &, base, size];
generatePowerSpiral[p_, nmax_] :=
Map[complexSplit, Table[tower[p, n], {n, 0, nmax-1, 1}]];
Manipulate[const = p[[1]] + p[[2]] I;
ListPlot[generatePowerSpiral[const, n],
PlotRange -> {{-2, 2}, {-2, 2}}, Axes -> ax,
Epilog -> Inset[Framed[const], {-1.5, -1.5}]], {{n, 100,
"Number of terms"}, 1, 200, 1,
Appearance -> "Labeled"}, {{ax, True, "Show axis"}, {True,
False}}, {{p, {0, 1.5}}, Locator}]
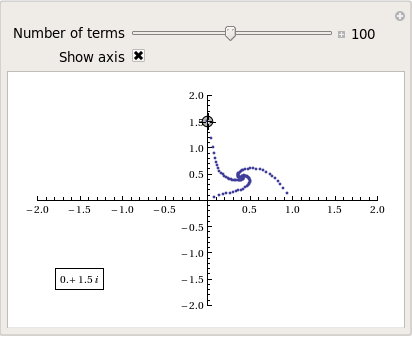
After playing around with this Manipulate for a few seconds it became clear to me that there is quite a rich diversity of these convergence spirals. Here are a couple more
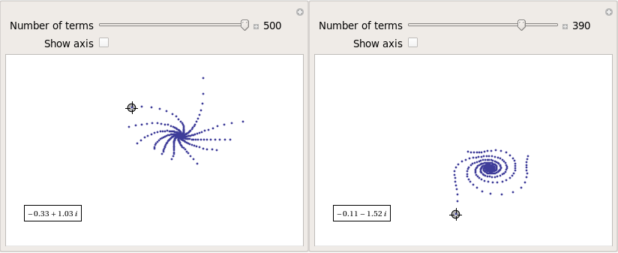
Some of them take a lot longer to converge than others and then there are those that don’t converge at all:
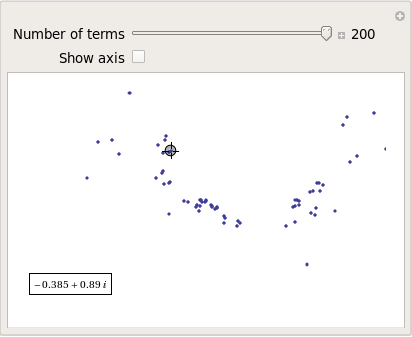
Optimising the code a little
Before I could investigate convergence any further, I had a problem to solve: Sometimes the Manipulate would completely freeze and a message eventually popped up saying “One or more dynamic objects are taking excessively long to finish evaluating……” What was causing this I wondered?
Well, some values give overflow errors:
In[12]:= generatePowerSpiral[-1 + -0.5 I, 200] General::ovfl: Overflow occurred in computation. >> General::ovfl: Overflow occurred in computation. >> General::ovfl: Overflow occurred in computation. >> General::stop: Further output of General::ovfl will be suppressed during this calculation. >>
Could errors such as this be making my Manipulate unstable? Let’s see how long it takes Mathematica to deal with the example above
AbsoluteTiming[ListPlot[generatePowerSpiral[-1 -0.5 I, 200]]]
On my machine, the above command typically takes around 0.08 seconds to complete compared to 0.04 seconds for a tower that converges nicely; it’s slower but not so slow that it should break Manipulate. Still, let’s fix it anyway.
Look at the sequence of values that make up this problematic power tower
generatePowerSpiral[-0.8 + 0.1 I, 10]
{{-0.8, 0.1}, {-0.668442, -0.570216}, {-2.0495, -6.11826},
{2.47539*10^7,1.59867*10^8}, {2.068155430437682*10^-211800874,
-9.83350984373519*10^-211800875}, {Overflow[], 0}, {Indeterminate,
Indeterminate}, {Indeterminate, Indeterminate}, {Indeterminate,
Indeterminate}, {Indeterminate, Indeterminate}}
Everything is just fine until the term {Overflow[],0} is reached; after which we are just wasting time. Recall that the functions I am using to create these sequences are
complexSplit[x_] := {Re[x], Im[x]};
tower[base_, size_] := Nest[N[(base^#)] &, base, size];
generatePowerSpiral[p_, nmax_] :=
Map[complexSplit, Table[tower[p, n], {n, 0, nmax-1, 1}]];
The first thing I need to do is break out of tower’s Nest function as soon as the result stops being a complex number and the NestWhile function allows me to do this. So, I could redefine the tower function to be
tower[base_, size_] := NestWhile[N[(base^#)] &, base, MatchQ[#, _Complex] &, 1, size]
However, I can do much better than that since my code so far is massively inefficient. Say I already have the first n terms of a tower sequence; to get the (n+1)th term all I need to do is a single power operation but my code is starting from the beginning and doing n power operations instead. So, to get the 5th term, for example, my code does this
I^I^I^I^I
instead of
(4th term)^I
The function I need to turn to is yet another variant of Nest – NestWhileList
fasttowerspiral[base_, size_] := Quiet[Map[complexSplit, NestWhileList[N[(base^#)] &, base, MatchQ[#, _Complex] &, 1, size, -1]]];
The Quiet function is there to prevent Mathematica from warning me about the Overflow error. I could probably do better than this and catch the Overflow error coming before it happens but since I’m only mucking around, I’ll leave that to an interested reader. For now it’s enough for me to know that the code is much faster than before:
(*Original Function*)
AbsoluteTiming[generatePowerSpiral[I, 200];]
{0.036254, Null}
(*Improved Function*)
AbsoluteTiming[fasttowerspiral[I, 200];]
{0.001740, Null}
A factor of 20 will do nicely!
Making Mathematica faster by making it stupid
I’m still not done though. Even with these optimisations, it can take a massive amount of time to compute some of these power tower spirals. For example
spiral = fasttowerspiral[-0.77 - 0.11 I, 100];
takes 10 seconds on my machine which is thousands of times slower than most towers take to compute. What on earth is going on? Let’s look at the first few numbers to see if we can find any clues
In[34]:= spiral[[1 ;; 10]]
Out[34]= {{-0.77, -0.11}, {-0.605189, 0.62837}, {-0.66393,
7.63862}, {1.05327*10^10,
7.62636*10^8}, {1.716487392960862*10^-155829929,
2.965988537183398*10^-155829929}, {1., \
-5.894184073663391*10^-155829929}, {-0.77, -0.11}, {-0.605189,
0.62837}, {-0.66393, 7.63862}, {1.05327*10^10, 7.62636*10^8}}
The first pair that jumps out at me is {1.71648739296086210^-155829929, 2.96598853718339810^-155829929} which is so close to {0,0} that it’s not even funny! So close, in fact, that they are not even double precision numbers any more. Mathematica has realised that the calculation was going to underflow and so it caught it and returned the result in arbitrary precision.
Arbitrary precision calculations are MUCH slower than double precision ones and this is why this particular calculation takes so long. Mathematica is being very clever but its cleverness is costing me a great deal of time and not adding much to the calculation in this case. I reckon that I want Mathematica to be stupid this time and so I’ll turn off its underflow safety net.
SetSystemOptions["CatchMachineUnderflow" -> False]
Now our problematic calculation takes 0.000842 seconds rather than 10 seconds which is so much faster that it borders on the astonishing. The results seem just fine too!
When do the power towers converge?
We have seen that some towers converge while others do not. Let S be the set of complex numbers which lead to convergent power towers. What might S look like? To determine that I have to come up with a function that answers the question ‘For a given complex number z, does the infinite power tower converge?’ The following is a quick stab at such a function
convergeQ[base_, size_] :=
If[Length[
Quiet[NestWhileList[N[(base^#)] &, base, Abs[#1 - #2] > 0.01 &,
2, size, -1]]] < size, 1, 0];
The tolerance I have chosen, 0.01, might be a little too large but these towers can take ages to converge and I’m more interested in speed than accuracy right now so 0.01 it is. convergeQ returns 1 when the tower seems to converge in at most size steps and 0 otherwise.:
In[3]:= convergeQ[I, 50] Out[3]= 1 In[4]:= convergeQ[-1 + 2 I, 50] Out[4]= 0
So, let’s apply this to a section of the complex plane.
towerFract[xmin_, xmax_, ymin_, ymax_, step_] :=
ArrayPlot[
Table[convergeQ[x + I y, 50], {y, ymin, ymax, step}, {x, xmin, xmax,step}]]
towerFract[-2, 2, -2, 2, 0.1]

That looks like it might be interesting, possibly even fractal, behaviour but I need to increase the resolution and maybe widen the range to see what’s really going on. That’s going to take quite a bit of calculation time so I need to optimise some more.
Going Parallel
There is no point in having machines with two, four or more processor cores if you only ever use one and so it is time to see if we can get our other cores in on the act.
It turns out that this calculation is an example of a so-called embarrassingly parallel problem and so life is going to be particularly easy for us. Basically, all we need to do is to give each core its own bit of the complex plane to work on, collect the results at the end and reap the increase in speed. Here’s the full parallel version of the power tower fractal code
(*Complete Parallel version of the power tower fractal code*)
convergeQ[base_, size_] :=
If[Length[
Quiet[NestWhileList[N[(base^#)] &, base, Abs[#1 - #2] > 0.01 &,
2, size, -1]]] < size, 1, 0];
LaunchKernels[];
DistributeDefinitions[convergeQ];
ParallelEvaluate[SetSystemOptions["CatchMachineUnderflow" -> False]];
towerFractParallel[xmin_, xmax_, ymin_, ymax_, step_] :=
ArrayPlot[
ParallelTable[
convergeQ[x + I y, 50], {y, ymin, ymax, step}, {x, xmin, xmax, step}
, Method -> "CoarsestGrained"]]
This code is pretty similar to the single processor version so let’s focus on the parallel modifications. My convergeQ function is no different to the serial version so nothing new to talk about there. So, the first new code is
LaunchKernels[];
This launches a set of parallel Mathematica kernels. The amount that actually get launched depends on the number of cores on your machine. So, on my dual core laptop I get 2 and on my quad core desktop I get 4.
DistributeDefinitions[convergeQ];
All of those parallel kernels are completely clean in that they don’t know about my user defined convergeQ function. This line sends the definition of convergeQ to all of the freshly launched parallel kernels.
ParallelEvaluate[SetSystemOptions["CatchMachineUnderflow" -> False]];
Here we turn off Mathematica’s machine underflow safety net on all of our parallel kernels using the ParallelEvaluate function.
That’s all that is necessary to set up the parallel environment. All that remains is to change Map to ParallelMap and to add the argument Method -> “CoarsestGrained” which basically says to Mathematica ‘Each sub-calculation will take a tiny amount of time to perform so you may as well send each core lots to do at once’ (click here for a blog post of mine where this is discussed further).
That’s all it took to take this embarrassingly parallel problem from a serial calculation to a parallel one. Let’s see if it worked. The test machine for what follows contains a T5800 Intel Core 2 Duo CPU running at 2Ghz on Ubuntu (if you want to repeat these timings then I suggest you read this blog post first or you may find the parallel version going slower than the serial one). I’ve suppressed the output of the graphic since I only want to time calculation and not rendering time.
(*Serial version*)
In[3]= AbsoluteTiming[towerFract[-2, 2, -2, 2, 0.1];]
Out[3]= {0.672976, Null}
(*Parallel version*)
In[4]= AbsoluteTiming[towerFractParallel[-2, 2, -2, 2, 0.1];]
Out[4]= {0.532504, Null}
In[5]= speedup = 0.672976/0.532504
Out[5]= 1.2638
I was hoping for a bit more than a factor of 1.26 but that’s the way it goes with parallel programming sometimes. The speedup factor gets a bit higher if you increase the size of the problem though. Let’s increase the problem size by a factor of 100.
towerFractParallel[-2, 2, -2, 2, 0.01]
The above calculation took 41.99 seconds compared to 63.58 seconds for the serial version resulting in a speedup factor of around 1.5 (or about 34% depending on how you want to look at it).

Other optimisations
I guess if I were really serious about optimising this problem then I could take advantage of the symmetry along the x axis or maybe I could utilise the fact that if one point in a convergence spiral converges then it follows that they all do. Maybe there are more intelligent ways to test for convergence or maybe I’d get a big speed increase from programming in C or F#? If anyone is interested in having a go at improving any of this and succeeds then let me know.
I’m not going to pursue any of these or any other optimisations, however, since the above exploration is what I achieved in a single train journey to work (The write-up took rather longer though). I didn’t know where I was going and I only worried about optimisation when I had to. At each step of the way the code was fast enough to ensure that I could interact with the problem at hand.
Being mostly ‘fast enough’ with minimal programming effort is one of the reasons I like playing with Mathematica when doing explorations such as this.
Treading where people have gone before
So, back to the power tower story. As I mentioned earlier, I did most of the above in a single train journey and I didn’t have access to the internet. I was quite excited that I had found a fractal from such a relatively simple system and very much felt like I had discovered something for myself. Would this lead to something that was publishable I wondered?
Sadly not!
It turns out that power towers have been thoroughly investigated and the act of forming a tower is called tetration. I learned that when a tower converges there is an analytical formula that gives what it will converge to:
![]()
Where W is the Lambert W function (click here for a cool poster for this function). I discovered that other people had already made Wolfram Demonstrations for power towers too
There is even a website called tetration.org that shows ‘my’ fractal in glorious technicolor. Nothing new under the sun eh?
Parting shots
Well, I didn’t discover anything new but I had a bit of fun along the way. Here’s the final Manipulate I came up with
Manipulate[const = p[[1]] + p[[2]] I;
If[hz,
ListPlot[fasttowerspiral[const, n], PlotRange -> {{-2, 2}, {-2, 2}},
Axes -> ax,
Epilog -> {{PointSize[Large], Red,
Point[complexSplit[N[h[const]]]]}, {Inset[
Framed[N[h[const]]], {-1, -1.5}]}}]
, ListPlot[fasttowerspiral[const, n],
PlotRange -> {{-2, 2}, {-2, 2}}, Axes -> ax]
]
, {{n, 100, "Number of terms"}, 1, 500, 1, Appearance -> "Labeled"}
, {{ax, True, "Show axis"}, {True, False}}
, {{hz, True, "Show h(z)"}, {True, False}}
, {{p, {0, 1.5}}, Locator}
, Initialization :> (
SetSystemOptions["CatchMachineUnderflow" -> False];
complexSplit[x_] := {Re[x], Im[x]};
fasttowerspiral[base_, size_] :=
Quiet[Map[complexSplit,
NestWhileList[N[(base^#)] &, base, MatchQ[#, _Complex] &, 1,
size, -1]]];
h[z_] := -ProductLog[-Log[z]]/Log[z];
)
]
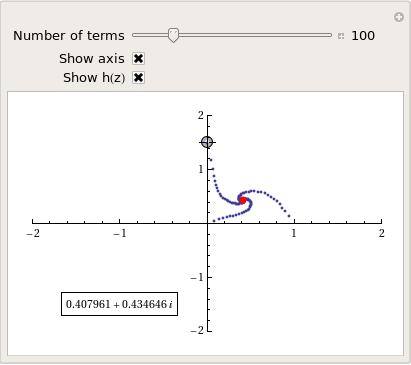
and here’s a video of a zoom into the tetration fractal that I made using spare cycles on Manchester University’s condor pool.
If you liked this blog post then you may also enjoy:
There have been a couple of blog posts recently that have focused on creating interactive demonstrations for the discrete logistic equation – a highly simplified model of population growth that is often used as an example of how chaotic solutions can arise in simple systems. The first blog post over at Division by Zero used the free GeoGebra package to create the demonstration and a follow up post over at MathRecreation used a proprietary package called Fathom (which I have to confess I have never heard of – drop me a line if you have used it and like it). Finally, there is also a Mathematica demonstration of the discrete logistic equation over at the Wolfram Demonstrations project.
I figured that one more demonstration wouldn’t hurt so I coded it up in SAGE – a free open source mathematical package that has a level of power on par with Mathematica or MATLAB. Here’s the code (click here if you’d prefer to download it as a file).
def newpop(m,prevpop):
return m*prevpop*(1-prevpop)
def populationhistory(startpop,m,length):
history = [startpop]
for i in range(length):
history.append( newpop(m,history[i]) )
return history
@interact
def _( m=slider(0.05,5,0.05,default=1.75,label='Malthus Factor') ):
myplot=list_plot( populationhistory(0.1,m,20) ,plotjoined=True,marker='o',ymin=0,ymax=1)
myplot.show()
Here’s a screenshot for a Malthus Factor of 1.75
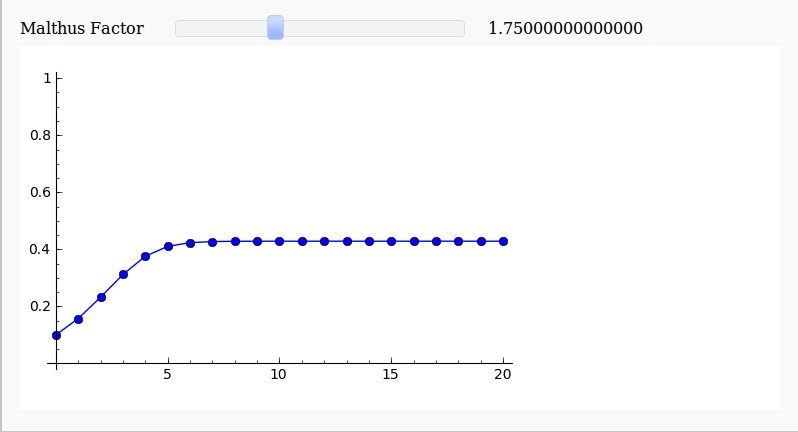
and here’s one for a Malthus Factor of 3.1
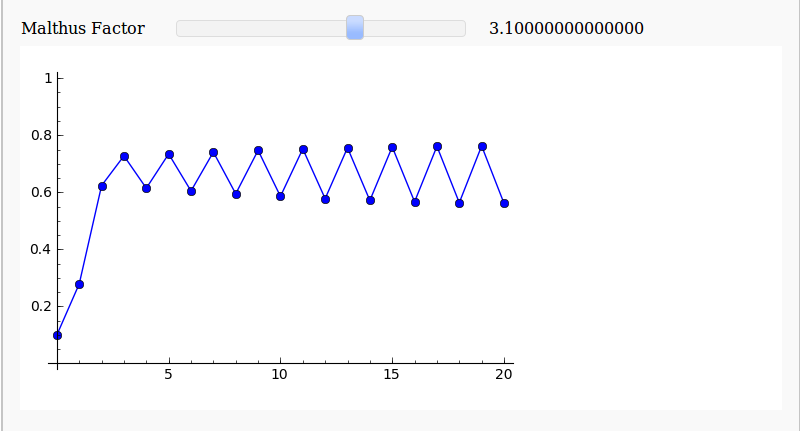
There are now so many different ways to easily make interactive mathematical demonstrations that there really is no excuse not to use them.
Update (11th December 2009)
As Harald Schilly points out, you can make a nice fractal out of this by plotting the limit points. My blogging software ruined his code when he placed it in the comments section so I reproduce it here (but he’s also uploaded it to sagenb)
var('x malthus')
step(x,malthus) = malthus * x * (1-x)
stepfast = fast_callable(step, vars=[x, malthus], domain=RDF)
def logistic(m, step):
# filter cycles
v = .5
for i in range(100):
v = stepfast(v,m)
points = []
for i in range(100):
v = stepfast(v,m)
points.append((m+step*random(),v))
return points
points=[] step = 0.005 for m in sxrange(2.5,4,step): points += logistic(m, step) point(points,pointsize=1).show(dpi=150)

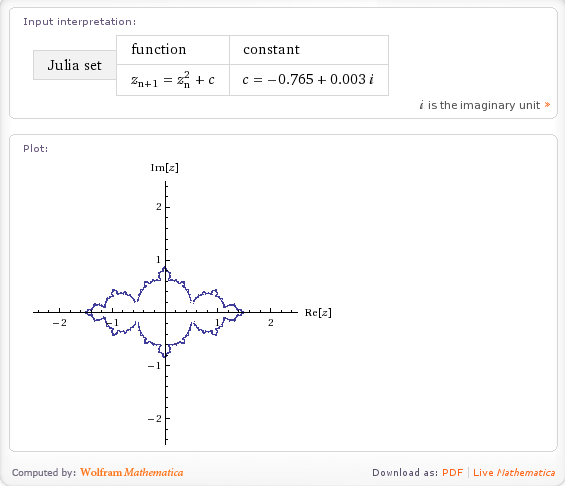
I saw a tweet from someone this morning which mentioned that you could plot the Julia Set using Wolfram Alpha. I had to try this for myself as soon as I could and, sure enough, you can plot the Julia set for any complex number Z: -0.765+0.003 I for example.
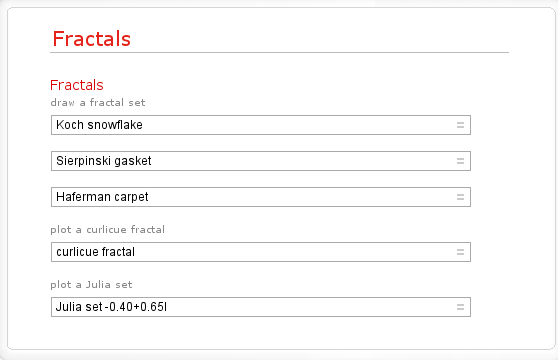
Very nice but what else can it do. If I Walpha fractals then I get the following output so I’d expect Wolfram Alpha to compute at least the Koch snow flake, the Sierpinski gasket, the Haferman carpet and the curlicue fractal and, sure enough, it does (click on the links to see for yourself)
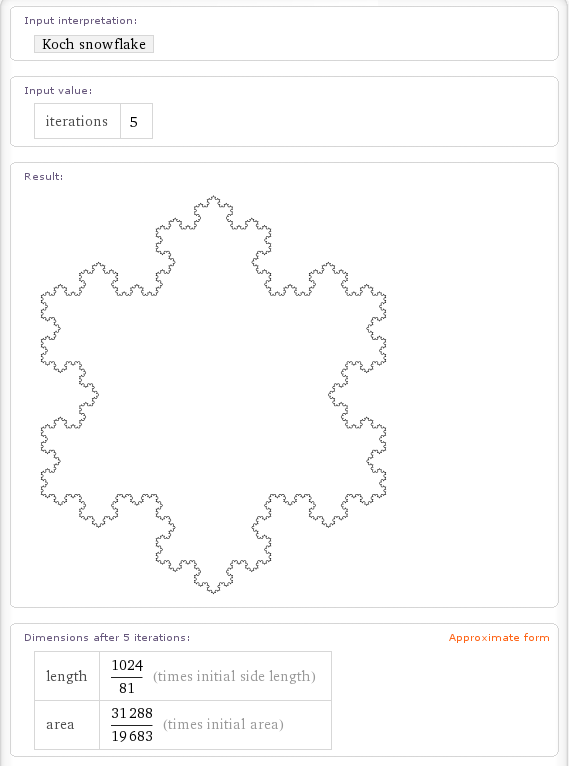
Here is a screenshot for the Koch Fractal.
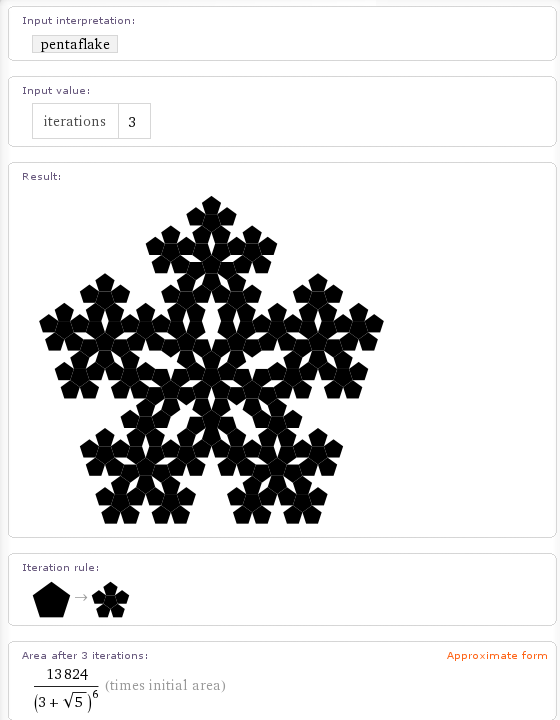
These aren’t the only fractals it knows about though. If you walpha Pentaflake (a fractal close to my heart) then you get the following.
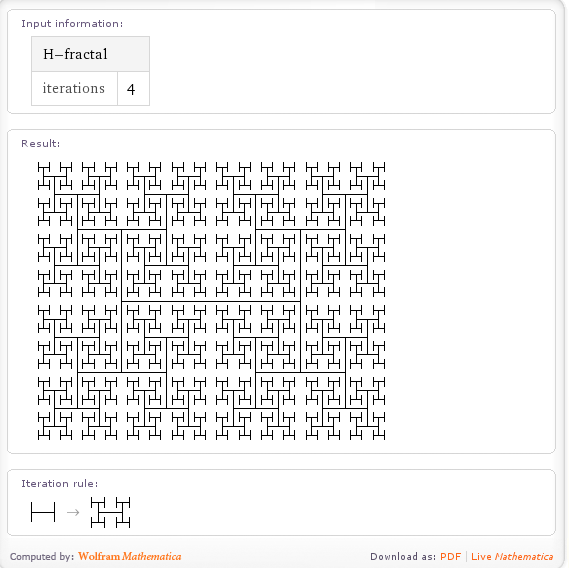
Wolfram Alpha can also calculate the H-Fractal.
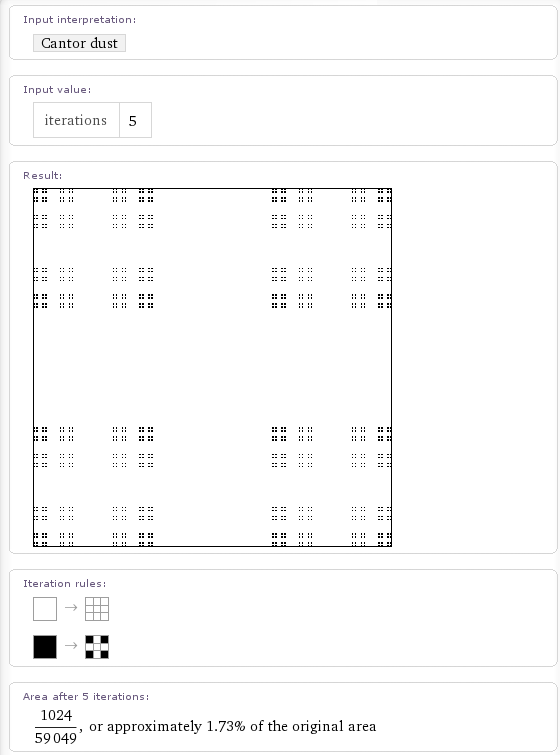
Cantor dust is in there too
as is the box fractal

It also looks like they are in the middle of implementing the Cesaro fractal. If you walpha the term then it tries to generate the fractal for a phase angle of pi/3 radians and 5 iterations. A few seconds later and the calculation times out. If you lower the number of iterations it returns a red box such as the one below. If my memory serves, Mathematica returns such a box if there is a problem with the graphics output. I hope to see this fixed soon.
Update:15th July 2009 – The Cesaro Fractal has now been fixed)
It also seems to know about the following fractals but doesn’t seem to calculate anything for them (yet). I say that it seems to know about them because it gives you an input field for ‘Iterations’ which implies that it knows that a number of iterations makes sense in this context. It’ll be cool to see all of these implemented in time.
(Note: None of these are implemented yet and may never be – I’ll update if that changes)
- Menger Sponge Update 21st December 2010 – this has now been implemented
- Gosper Island Update:15th July 2009 – this has now been implemented
- Apollonian Gasket Update 21st December 2010 – this has now been implemented
- Dragon Curve Update 21st December 2010 – this has now been implemented
- Hilbert Curve Update 21st December 2010 – this has now been implemented
- Peano curve Update 21st December 2010 – this has now been implemented
- Cantor Set Update:15th July 2009 – this has now been implemented
Some odd omissions (at the time of writing) are the Mandelbrot set (Update: 15th July 2009 – this has been done now) and the Lorenz attractor.
This is all seriously cool stuff for Fractal fans and shows the power of the Wolfram Alpha idea. Let me know if you discover any more Fractals that it knows about and I’ll add them here.
Update: I’ve found a few more computable fractals in Wolfram Alpha. Please forgive me for the lack of screenshots but this is getting to be a rather graphic-intensive post. The links will take you to a Wolfram Alpha query.
Here in the UK we have had more snow than we have seen in over 20 years and as a country we are struggling with it to say the least. I have friends in places such as Finland who think that all this is rather funny…it takes nothing more than a bit of snow to bring the UK to its knees.
Anyway…all this talk of snow reminds me of a Wolfram Demonstration I authored around Christmas time called n-flakes. It started off while I was playing with the so called pentaflake which was first described by someone called Albrecht Dürer (according to Wolfram’s Mathworld). To make a pentaflake you first start of with a pentagon like this one.

Your next step is to get five more identical pentagons and place each one around the edges of the first as follows

The final result is the first iteration of the pentaflake design. Take a closer look at it….notice how the outline of the pentaflake is essentially a pentagon with some gaps in it?

Lets see what happens if we take this ‘gappy’ pentagon and arrange 5 identical gappy pentagons around it – just like we did in the first iteration.

The end result is a more interesting looking gappy pentagon. If we keep going in this manner then you eventually end up with something like this

Which is very pretty I think. Anyway, over at Mathworld, Eric Weisstein had written some Mathematica code to produce not only this variation of a pentaflake but also another one which was created by putting pentagons at the corners of the first one rather than the sides. Also, rather than using identical pentagons, this second variation used scaled pentagons for each iteration. The end result is shown below.

Looking at Eric’s code I discovered that it would be a trivial matter to wrap this up in a Manipulate function and produce an interactive version. This took about 30 seconds – the quickest Wolfram demonstration I had ever written. After submitting it (with due credit being given to Eric) I got an email back from the Wolfram Demonstration team saying ‘Why stop at just pentagons? Could you generalise it a bit before we publish it?’
So I did and the result was named N-flakes which is available for download on the Wolfram Demonstrations site. Along with pentaflakes, you can also play with hexaflakes, quadraflakes and triflakes. One or two of these usually go by slightly different names – kudos for anyone who finds them.