Walking Randomly

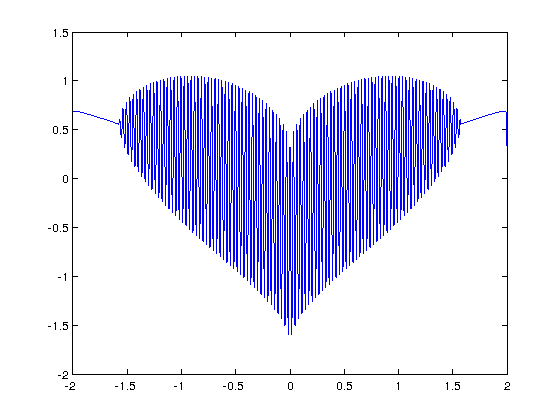
I’ve seen several equations that plot a heart shape over the years but a recent google+ post by Lionel Favre introduced me to a new one.  I liked it so much that I didn’t want to wait until Valentine’s day to share it.  In Mathematica:

Plot[Sqrt[Cos[x]]*Cos[200*x] + Sqrt[Abs[x]] - 0.7*(4 - x*x)^0.01, {x, -2, 2}]

and in MATLAB:

>> x=[-2:.001:2];
>> y=(sqrt(cos(x)).*cos(200*x)+sqrt(abs(x))-0.7).*(4-x.*x).^0.01;
>> plot(x,y)
Warning: Imaginary parts of complex X and/or Y arguments ignored

The result from the MATLAB version is shown below

Update

Rene Grothmann has looked at this equation in a little more depth and plotted it using Euler.

Similar posts

• A little mathematics for Valentine’s day
• The equation that says Hi

Welcome to the final Month of Math Software for 2011.  Lots of people sent in news items this month so hopefully there will be something of interest to everyone.  If you have any news items or articles that you think will fit in to next month’s edition then please contact me and tell me all about it.

If you like what you see and want more then check out the archives.

Mathematica StackExchange Proposal

There is a proposal to launch a new Mathematica-specific questions/answers site on StackExchange.  All it needs is enough interested people who will follow or commit to the proposal. There is already a vibrant Mathematica community on StackOverflow, where many of the MathGroup regulars participate.  Unfortunately not all questions are on topic or tolerated there, so many believe that it would be better to launch a new site.  If you are willing to lend support to this proposal then add your name to the list at  http://area51.stackexchange.com/proposals/37304/mathematica?referrer=23yK9sXkBPQIDM_9uBjtlA2

General mathematical software

• Version 5.26 of Maxima, a free computer algebra system for Windows, Linux and Mac OS X, has been released over at Sourceforge.  No details on what’s new yet.
• The free, open-source stats software, R, has seen a minor update with 2.14.1.  Full details of the new stuff can be found at https://stat.ethz.ch/pipermail/r-announce/2011/000548.html
• The free Euler Math Toolbox is now at version 13.3.  See what’s new at http://eumat.sourceforge.net/versions/version-13.html
• The general purpose computational algebra system, Magma, has been updated to version 2.18.2.  See what’s new at http://magma.maths.usyd.edu.au/magma/releasenotes/2/18/2/

Making MATLAB faster

• Jacket, the GPU accelerated toolbox for MATLAB from Accelereyes, has seen a major update.  Version 2.0 includes all sorts of new goodies including faster random number generation, improved multi-GPU support, and a load of new functions.  Perhaps most importantly, Jacket 2.0 includes support for OpenCL which opens the product up to many more hardware configurations. See more details on what’s new at their wiki.
• I wrote a blog post that demonstrates how to use Intel’s SPMD Program Compiler, ispc, to write faster mex files in MATLAB.

More mathematics in CUDA

• Release candidate 2 of version 4.1 of NVIDIA’s CUDA Toolkit has been released.  There’s lots of interesting new mathmatical functions and enhancements over version 4.0 including Bessel functions, a new cuSPARSE tri-diagonal solver, new random number generators (MRG32k3a and MTGP11213 Mersenne Twister), and one thousand image processing functions!

Differential Equations

• FEniCS 1.0 has been released.  The FEniCS Project is a collection of free software with an extensive list of features for automated, efficient solution of differential equations.

Libraries

• The HSL Mathematical Software Library (http://www.hsl.rl.ac.uk) is a high performance Fortran library that specialises in sparse linear algebra and is widely used by engineering and optimization communities. Since the release of HSL 2011 at the start of Feburary, there have been a number of updates to the library.  Take a look at http://www.hsl.rl.ac.uk/changes.html for the detailed list of changes.  Interestingly, this library is free for academic use!
• FLINT (Fast Library for Number Theory) version 2.3alpha has been released.  I can’t find any info on what’s new at the moment.
• Version 5.1 of AMDs linear algebra library, ACML, is now available.
• Version 1.6 of the AMD Accelerated Parallel Processing Math Libraries (APPML) has been released.  I’m not sure what’s new since the release notes only contain information about Timeout Detection and Recovery rather than info on the new stuff.  AMD Accelerated Parallel Processing Math Libraries are software libraries containing FFT and BLAS functions written in OpenCL and designed to run on AMD GPUs. The libraries also support running on CPU devices to facilitate debugging and multicore programming.
• Version 2.4.5 of PLASMA (Parallel Linear Algebra for Scalable Multi-core Architectures) was released back in November but I somehow missed it.  Check out the 2.4.5 release notes for details.

Blog posts about Mathematical software

• Over at No Ice in my Scotch Please, stu has written a series of posts on how to leverage CUDA with MATLAB in Some Useful Tools for Numerical Solution of PDEs on a Workstation.
• Anna looks at 3D plots in the upcoming Mathcad prime 2.0.
• Arthur Charpentier uses R to explain how to use Markov chains to improve your Snakes and Ladders game :)
• Jon McLoone writes 10 Tips for Writing Fast Mathematica code. If this interests you then you may also be interested in my detailed look at Mathematica’s Compile function.
• Kyle demonstrates how reordering sparse matrices can improve parallelism.

Modern CPUs are capable of parallel processing at multiple levels with the most obvious being the fact that a typical CPU contains multiple processor cores.  My laptop, for example, contains a quad-core Intel Sandy Bridge i7 processor and so has 4 processor cores. You may be forgiven for thinking that, with 4 cores, my laptop can do up to 4 things simultaneously but life isn’t quite that simple.

The first complication is hyper-threading where each physical core appears to the operating system as two or more virtual cores.  For example, the processor in my laptop is capable of using hyper-threading and so I have access to up to 8 virtual cores!  I have heard stories where unscrupulous sales people have passed off a 4 core CPU with hyperthreading as being as good as an 8 core CPU…. after all, if you fire up the Windows Task Manager you can see 8 cores and so there you have it!  However, this is very far from the truth since what you really have is 4 real cores with 4 brain damaged cousins.  Sometimes the brain damaged cousins can do something useful but they are no substitute for physical cores.  There is a great explanation of this technology at makeuseof.com.

The second complication is the fact that each physical processor core contains a SIMD (Single Instruction Multiple Data) lane of a certain width. SIMD lanes, aka  SIMD units or vector units, can process several numbers simultaneously with a single instruction rather than only one a time.  The 256-bit wide SIMD lanes on my laptop’s processor, for example, can operate on up to 8 single (or 4 double) precision numbers per instruction.  Since each physical core has its own SIMD lane this means that a 4 core processor could theoretically operate on up to 32 single precision (or 16 double precision) numbers per clock cycle!

So, all we need now is a way of programming for these SIMD lanes!

Intel’s SPMD Program Compiler, ispc, is a free product that allows programmers to take direct advantage of the SIMD lanes in modern CPUS using a C-like syntax.  The speed-ups compared to single-threaded code can be impressive with Intel reporting up to 32 times speed-up (on an i7 quad-core) for a single precision Black-Scholes option pricing routine for example.

Using ispc on MATLAB

Since ispc routines are callable from C, it stands to reason that we’ll be able to call them from MATLAB using mex.  To demonstrate this, I thought that I’d write a sqrt function that works faster than MATLAB’s built-in version.  This is a tall order since the sqrt function is pretty fast and is already multi-threaded.  Taking the square root of 200 million random numbers doesn’t take very long in MATLAB:

>> x=rand(1,200000000)*10;
>> tic;y=sqrt(x);toc
Elapsed time is 0.666847 seconds.

This might not be the most useful example in the world but I wanted to focus on how to get ispc to work from within MATLAB rather than worrying about the details of a more interesting example.

Step 1 – A reference single-threaded mex file

Before getting all fancy, let’s write a nice, straightforward single-threaded mex file in C and see how fast that goes.

#include <math.h>
#include "mex.h"

void mexFunction( int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[] )
{
    double *in,*out;
    int rows,cols,num_elements,i; 

    /*Get pointers to input matrix*/
    in = mxGetPr(prhs[0]);
    /*Get rows and columns of input matrix*/
    rows = mxGetM(prhs[0]);
    cols = mxGetN(prhs[0]);
    num_elements = rows*cols;

    /* Create output matrix */
    plhs[0] = mxCreateDoubleMatrix(rows, cols, mxREAL);
    /* Assign pointer to the output */
    out = mxGetPr(plhs[0]);

    for(i=0; i<num_elements; i++)
    {
        out[i] = sqrt(in[i]);
    }
}

Save the above to a text file called sqrt_mex.c and compile using the following command in MATLAB

 mex sqrt_mex.c

Let’s check out its speed:

>> x=rand(1,200000000)*10;
>> tic;y=sqrt_mex(x);toc
Elapsed time is 1.993684 seconds.

Well, it works but it’s quite a but slower than the built-in MATLAB function so we still have some work to do.

Step 2 – Using the SIMD lane on one core via ispc

Using ispc is a two step process.  First of all you need the .ispc program

export void ispc_sqrt(uniform double vin[], uniform double vout[],
                   uniform int count) {
    foreach (index = 0 ... count) {
        vout[index] = sqrt(vin[index]);
    }
}

Save this to a file called ispc_sqrt.ispc and compile it at the Bash prompt using

ispc -O2 ispc_sqrt.ispc -o ispc_sqrt.o -h ispc_sqrt.h --pic

This creates an object file, ispc_sqrt.o, and a header file, ispc_sqrt.h. Now create the mex file in MATLAB

#include <math.h>
#include "mex.h"
#include "ispc_sqrt.h"

void mexFunction( int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[] )
{
    double *in,*out;
    int rows,cols,num_elements,i; 

    /*Get pointers to input matrix*/
    in = mxGetPr(prhs[0]);
    /*Get rows and columns of input matrix*/
    rows = mxGetM(prhs[0]);
    cols = mxGetN(prhs[0]);
    num_elements = rows*cols;

    /* Create output matrix */
    plhs[0] = mxCreateDoubleMatrix(rows, cols, mxREAL);
    /* Assign pointer to the output */
    out = mxGetPr(plhs[0]);

    ispc::ispc_sqrt(in,out,num_elements);
}

Call this ispc_sqrt_mex.cpp and compile in MATLAB with the command

 mex ispc_sqrt_mex.cpp ispc_sqrt.o

Let’s see how that does for speed:

>> tic;y=ispc_sqrt_mex(x);toc
Elapsed time is 1.379214 seconds.

So, we’ve improved on the single-threaded mex file a bit (1.37 instead of 2 seconds) but it’s still not enough to beat the MATLAB built-in.  To do that, we are going to have to use the SIMD lanes on all 4 cores simultaneously.

Step 3 – A reference multi-threaded mex file using OpenMP

Let’s step away from ispc for a while and see how we do with something we’ve seen before– a mex file using OpenMP (see here and here for previous articles on this topic).

#include <math.h>
#include "mex.h"
#include <omp.h>

void do_calculation(double in[],double out[],int num_elements)
{
    int i;

#pragma omp parallel for shared(in,out,num_elements)
    for(i=0; i<num_elements; i++){
          out[i] = sqrt(in[i]);
         }
}

void mexFunction( int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[] )
{
    double *in,*out;
    int rows,cols,num_elements,i; 

    /*Get pointers to input matrix*/
    in = mxGetPr(prhs[0]);
    /*Get rows and columns of input matrix*/
    rows = mxGetM(prhs[0]);
    cols = mxGetN(prhs[0]);
    num_elements = rows*cols;

    /* Create output matrix */
    plhs[0] = mxCreateDoubleMatrix(rows, cols, mxREAL);
    /* Assign pointer to the output */
    out = mxGetPr(plhs[0]);

    do_calculation(in,out,num_elements);
}

Save this to a text file called openmp_sqrt_mex.c and compile in MATLAB by doing

 mex openmp_sqrt_mex.c CFLAGS="\$CFLAGS -fopenmp" LDFLAGS="\$LDFLAGS -fopenmp"

Let’s see how that does (OMP_NUM_THREADS has been set to 4):

>> tic;y=openmp_sqrt_mex(x);toc
Elapsed time is 0.641203 seconds.

That’s very similar to the MATLAB built-in and I suspect that The Mathworks have implemented their sqrt function in a very similar manner. Theirs will have error checking, complex number handling and what-not but it probably comes down to a for-loop that’s been parallelized using Open-MP.

Step 4 – Using the SIMD lanes on all cores via ispc

To get a ispc program to run on all of my processors cores simultaneously, I need to break the calculation down into a series of tasks. The .ispc file is as follows

task void
ispc_sqrt_block(uniform double vin[], uniform double vout[],
                   uniform int block_size,uniform int num_elems){
    uniform int index_start = taskIndex * block_size;
    uniform int index_end = min((taskIndex+1) * block_size, (unsigned int)num_elems);

    foreach (yi = index_start ... index_end) {
        vout[yi] = sqrt(vin[yi]);
    }
}

export void
ispc_sqrt_task(uniform double vin[], uniform double vout[],
                   uniform int block_size,uniform int num_elems,uniform int num_tasks)
{

    launch[num_tasks] < ispc_sqrt_block(vin, vout, block_size, num_elems) >;
}

Compile this by doing the following at the Bash prompt

ispc -O2 ispc_sqrt_task.ispc -o ispc_sqrt_task.o -h ispc_sqrt_task.h --pic

We’ll need to make use of a task scheduling system. The ispc documentation suggests that you could use the scheduler in Intel’s Threading Building Blocks or Microsoft’s Concurrency Runtime but a basic scheduler is provided with ispc in the form of tasksys.cpp (I’ve also included it in the .tar.gz file in the downloads section at the end of this post), We’ll need to compile this too so do the following at the Bash prompt

g++ tasksys.cpp -O3 -Wall -m64 -c -o tasksys.o -fPIC

Finally, we write the mex file

#include <math.h>
#include "mex.h"
#include "ispc_sqrt_task.h"

void mexFunction( int nlhs, mxArray *plhs[], int nrhs, const mxArray *prhs[] )
{
    double *in,*out;
    int rows,cols,i;

    unsigned int num_elements;
    unsigned int block_size;
    unsigned int num_tasks; 

    /*Get pointers to input matrix*/
    in = mxGetPr(prhs[0]);
    /*Get rows and columns of input matrix*/
    rows = mxGetM(prhs[0]);
    cols = mxGetN(prhs[0]);
    num_elements = rows*cols;

    /* Create output matrix */
    plhs[0] = mxCreateDoubleMatrix(rows, cols, mxREAL);
    /* Assign pointer to the output */
    out = mxGetPr(plhs[0]);

    block_size = 1000000;
    num_tasks = num_elements/block_size;

    ispc::ispc_sqrt_task(in,out,block_size,num_elements,num_tasks);

}

In the above, the input array is divided into tasks where each task takes care of 1 million elements. Our 200 million element test array will, therefore, be split into 200 tasks– many more than I have processor cores. I’ll let the task scheduler worry about how to schedule these tasks efficiently across the cores in my machine. Compile this in MATLAB by doing

mex ispc_sqrt_task_mex.cpp ispc_sqrt_task.o tasksys.o

Now for crunch time:

>> x=rand(1,200000000)*10;
>> tic;ys=sqrt(x);toc   %MATLAB's built-in
Elapsed time is 0.670766 seconds.
>> tic;y=ispc_sqrt_task_mex(x);toc  %my version using ispc
Elapsed time is 0.393870 seconds.

There we have it! A version of the sqrt function that works faster than MATLAB’s own by virtue of the fact that I am now making full use of the SIMD lanes in my laptop’s Sandy Bridge i7 processor thanks to ispc.

Although this example isn’t very useful as it stands, I hope that it shows that using the ispc compiler from within MATLAB isn’t as hard as you might think and is yet another tool in the arsenal of weaponry that can be used to make MATLAB faster.

Final Timings, downloads and links

• Single threaded: 2.01 seconds
• Single threaded with ispc: 1.37 seconds
• MATLAB built-in: 0.67 seconds
• Multi-threaded with OpenMP (OMP_NUM_THREADS=4): 0.64 seconds
• Multi-threaded with OpenMP and hyper-threading (OMP_NUM_THREADS=8): 0.55 seconds
• Task-based multicore with ispc: 0.39 seconds

Finally, here’s some links and downloads

• Download source-code for all examples
• Intel’s ispc compiler

System Specs

• MATLAB 2011b running on 64 bit linux
• gcc 4.6.1
• ispc version 1.1.1
• Intel Core i7-2630QM with 8Gb RAM

Welcome to Walking Randomly’s monthly look at what’s new in the world of mathematical software.  Click here for last month’s edition and check out the archive for all previous editions.  If you have some news about mathematical software and want to get it out to over 2,500 subscribers then contact me and tell me all about it.

General mathematical software

• Python(x,y) has been updated to version 2.7.2.1.  Python(x,y) is a free scientific and engineering development software for numerical computations, data analysis and data visualization
• Version 2.17-13 of the number theoretic package, Magma, has been released.  Click here to see what’s new.
• Freemat, a a free environment for rapid engineering,scientific prototyping and data processing similar to MATLAB, has seen its first major update in 2 years!  The big news in version 4.1 is a Just In Time (JIT) compiler which should speed up code execution a great deal.  There is also a significant improvement in Freemat’s ability to render multidimensional datasets thanks to integration of the Visualisation Toolkit (VTK).
• The Euler Math Toolbox has been updated to version 13.1.  See the list of changes for details of what’s new.
• Gnumeric saw a new major release in November with 1.11.0 (click here for changes) closely followed by some bug fixes in 1.11.1 (changes here).  Gnumeric is a free spreadsheet program for Linux and Windows.

Linear Algebra

• LAPACK, The Fortran based linear algebra library that forms the bedrock of functionality in countless software applications,  has been updated to version 3.4.0.  Click here for the release notes.
• MAGMA, A linear algebra library that is “similar to LAPACK but for heterogeneous/hybrid architectures, starting with current “Multicore+GPU” systems.” has been updated to version 1.1
• PLASMA, The Parallel Linear Algebra for Scalable Multi-core Architectures, has been updated to version 2.4.5.  Click here for what’s new.

New Products

• AccelerEyes have released a new product called ArrayFire – a free CUDA and OpenCL library for C, C++, Fortran, and Python
• CULA Tools released a new product called CULA Sparse which is a GPU-accelerated library for linear algebra that provides iterative solvers for sparse systems.  They’ve also released a demo application to allow you to try the product out for free.

Vital Statistics

• R version 2.14.0 has been released with a host of new features.  If you do any kind of statistical computing then R is the free, open source solution for you!

Pretty plots

• Originlabs have updated their commercial windows plotting packages, Origin and OriginPro to version 8.6.  Here’s the press release.
• A new incremental update of GNUPlot, a free multiplatform plotting package, has been released.  The release announcement tells us what new goodies we get in version 4.4.4.

Mobile

• One of the best mobile mathematical applications that money can buy, SpaceTime, has released a new version for iOS and Mac OS X and changed its name to Math Studio.  Not to be confused with SMathStudio, another mobile mathematical application that is a clone of MathCad.
• The guys behind the excellent Android based Python/Sympy app – MathScript – have released a beta of a new product called ScriptBlocks.

Odds and ends

• RougeWave Software have released version 8.0 of the commercial IMSL C library.  Improvements include CUDA BLAS integration and a few new functions.  The full list is available on the what’s new page.
• Bernard Liengme has written a Primer for SmathStudio (a free Mathcad clone)
• Eureqa, a software tool for detecting equations and hidden mathematical relationships in your data, has seen a major new update: Eureqa II (Code Name Formulize).  Get it from http://creativemachines.cornell.edu/eureqa_download
• The Numerical Algorithms Group (NAG) have put together a set of examples where various versions of their numerical library product (for Fortran, C and .NET) are used in Labview programs.
• Scipy version 0.10.0 has been released.  Check out the release notes for the new stuff.

I recently spent a lot of time optimizing a MATLAB user’s code and made extensive use of mex files written in C.  Now, one of the habits I have gotten into is to mix C and C++ style comments in my C source code like so:

/* This is a C style comment */

// This is a C++ style comment

For this particular project I did all of the development on Windows 7 using MATLAB 2011b and Visual Studio 2008 which had no problem with my mixing of comments. Move over to Linux, however, and it’s a very different story. When I try to compile my mex file

mex block1.c -largeArrayDims 

I get the error message

block1.c:48: error: expected expression before ‘/’ token

The fix is to call mex as follows:

mex block1.c -largeArrayDims CFLAGS="\$CFLAGS -std=c99"

Hope this helps someone out there. For the record, I was using gcc and MATLAB 2011a on 64bit Scientific Linux.