Archive for November, 2009
One of the benefits of writing a blog is that people write to me and tell me all kinds of interesting things. For example, early this morning a colleague of mine sent me the details of a bug in MATLAB 2009b which you can reproduce as follows.
A=[ 0 2 ; 1 0 ]; b=[ 2 ; 0 ]; A'\b ans = 0 1
which is, quite simply, wrong! The previous version of MATLAB, MATLAB 2009a, (along with MATLAB’s free clone – Octave) gets it right though:
ans = 0 2
so this is a new bug. Curiously, there is no problem with other matrices. For example the following, correct, result is given by 2009b:
A = [1 2 ; 1 1] A'\b ans = -2 4
In case you don’t speak MATLAB, the command A’\b solves the matrix equation ATx = b for an unknown vector, x. If you speak Mathematica then the equivalent command is
LinearSolve[Transpose[A], b]
Now, the MATLAB command transpose(A)\b is syntactically equivalent to A’\b and yet the former gives the correct result in this particular case:
transpose(A)\b ans = 0 2
What I find interesting about this particular bug is that it involves one of MATLAB’s core areas of functionality – solving linear systems. I wonder what readers of this blog think about it? Is it a trivial bug that is unlikely to cause problems in the real world or is it something that we should be worried about?
Many thanks to Frank Schmidt who discovered this bug and gave me permission to copy his findings wholesale and also thanks to my colleague Chris Paul who made me aware of it.
Update 1 (1st December 2009): Thanks to ‘Zebb Prime’ who reminded me that ‘ is equivalent to the complex transpose – ctranspose() – and not transpose() as I put in the post above. I got away with it in my post because we are dealing with real numbers. This mistake doesn’t alter the fact that there is a bug. The equivalent Mathematica code should be
LinearSolve[Conjugate[Transpose[A]], b]
I’ve been getting emails recently from people asking if I can mirror my RSS feed onto a twitter account since they look at Twitter more than Google Reader! Not wanting to disappoint, I have created a Twitter feed just for Walking Randomly called, predictably enough, @walkingrandomly. The new feed will include links to all new Walking Randomly articles as they happen and will also be supplemented by links to other websites that I find interesting.
If you are interested in hooking your RSS feed to a Twitter account in this manner then check out Twitterfeed.com.
One of the problems with the Linux MATLAB installer is that it doesn’t add any items to the menu in windows managers such as GNOME or KDE so you have to do it manually. Now, there are several ways to do this but one of the easiest is to use the GUI tools provided with Ubuntu (assuming you are using Ubuntu of course). For the record I am using Ubuntu 9.10 (Karmic Koala) with the default GNOME windows manager along with MATLAB 2009b but I imagine that these instructions will work for a few other configurations too.
First things first, you’ll want to download a nice, scalable MATLAB icon since the ones included with MATLAB itself are a bit crude to say the least. I tried to create one directly from MATLAB using the logo command and the Scalable Vector Graphics (SVG) Export of Figures package on The File Exchange but the result wasn’t very good (see below).

Fortunately someone called malte has created a much nicer .svg file (using inkscape) that looks just like the MATLAB logo and made it available via his blog.
Once you have the svg file you can start creating the shortcut as follows:
- On the GNOME Desktop click on System->Preferences->Main Menu
- Once the Main Menu program has started choose where you want your MATLAB icon to go and click on New Item. In the screenshot below I have started to put it in the Programming submenu.
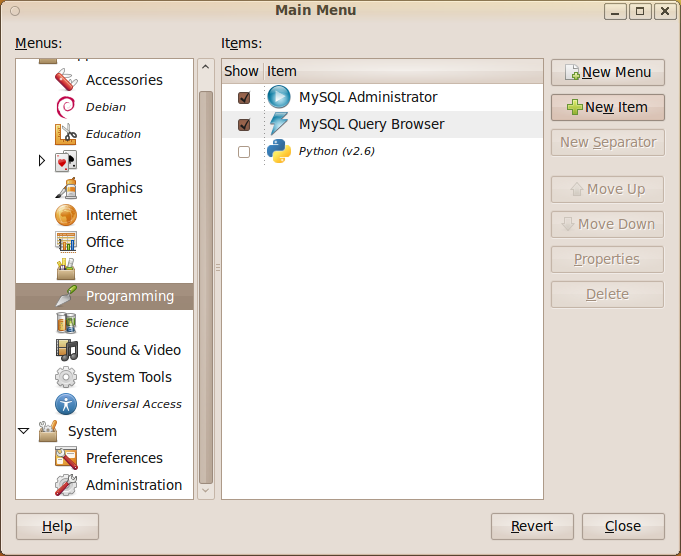
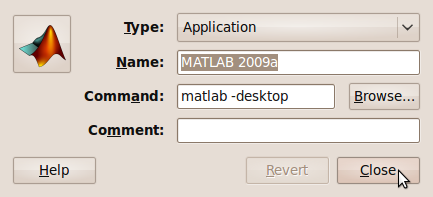
- Give your shortcut a name and put matlab -desktop in the command field. If you didn’t create a shortcut to the matlab executable when you installed the program then you may need to put the full path in instead (i.e. something like /opt/MATLAB/2009b/bin/matlab )

- Now let’s sort out the icon. Click on the spring on the left hand side of the above window to get the window below.
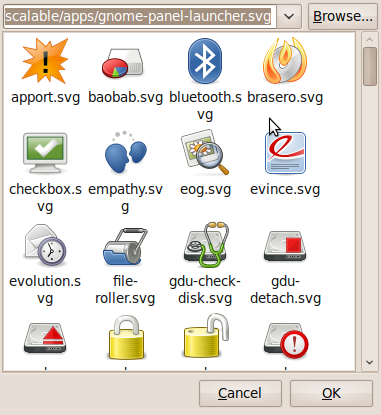
- Click on Browse and then select the folder that contains the .svg file you downloaded from malte’s blog. I put it in my Desktop folder for the screenshot below. Note that the svg file doesn’t appear in the preview pane. Click on Open.
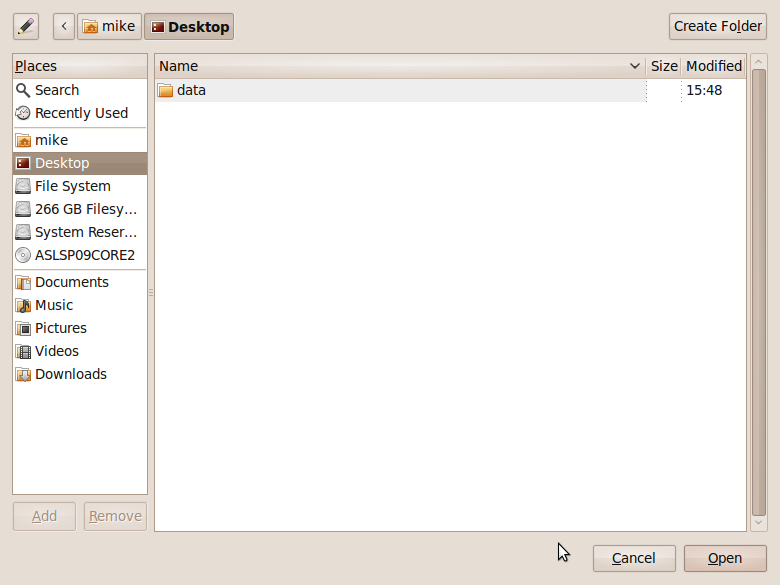
- Choose your icon.

- Click on Close and you are done
If you are using the Student version of MATLAB then the process is slightly different and has been covered by my friend Paul Brabban over at CrossedStreams.com.
There was a discussion recently on comp.soft-sys.math.mathematica about maintaining a user-led Mathematica bug list and various solutions were proposed. I have no desire (and certainly no time) to even try to maintain a ‘proper’ bug database for Mathematica but I am interested in maintaining a list of bugs that I personally find interesting and that I would like to see explained or fixed.
This post is that list.
First – some answers to potential questions.
Why are you doing this? I thought you liked Mathematica.
I love Mathematica but, like all pieces of software, it is not perfect. I find (some of) the imperfections interesting and since I get lots of hits from google every month from people looking for bugs in MATLAB, Mathematica, Maple, Mathcad etc then I assume that I am not alone. Every bug that I discuss here will be submitted to Wolfram Research and I will also update the page when the bug gets fixed.
I emailed/wrote a comment about a bug and you haven’t included it in the list. Why?
Sorry about that – please don’t take it personally. I am low on time and may not have managed to verify the ‘bug’ or maybe it just didn’t tickle my fancy. It’s also possible that I simply don’t understand the problem you are referring to and I will not post anything on here that I don’t at least think I understand. Remember – I’m not trying to keep a list of all Mathematica bugs – just some of the ones that I find interesting.
One of the ‘bugs’ you posted is not a bug – you just misunderstood the situation.
Oops, sorry! Please educate me so I can update it.
I think I have found a bug in Mathematica – what should I do?
In the first instance I suggest you post it to comp.soft-sys.math.mathematica – there are plenty of people there who know a lot about Mathematica and they (probably) will let you know if you really have found a bug or not. If everyone suspects that it is a bug then your next step is to report it to Wolfram. Finally, if you think I’d like to know about it then feel free to leave a comment to this post or email me.
FullSimplify bug 1
Clear[n]; FullSimplify[n Exp[-n * 0.], Element[n, Integers]]
expected output:
n
actual output:
n/2
original source – here.
Integrate bug 1
Integrate[k^2 (k^2 - 1)/((k^2 - 1)^2 + x^2)^(3/2), {k, 0, Infinity},Assumptions -> x > 0]
Expected output:
1/2*1/(1+x^2)^(1/4)*EllipticK(1/2*2^(1/2)*(((1+x^2)^(1/2)+1)/(1+x^2)^(1/2))^(1/2))
Actual output:
EllipticK[(2*x)/(-I + x)]/(2*Sqrt[-1 - I*x])
Note that although the integrand is real for all k, Mathematica gives a complex result which is clearly wrong. Original source – here.
Limit bug 1
Limit[EllipticTheta[3, 0, x], x -> 1, Direction -> 1]
Expected Output:
Infinity
Actual Output:
0
Original Source: here
NetworkFlow bug
The following code should complete in less than a second.
<< "Combinatorica`" NetworkFlow[CompleteGraph[4, 4], 1, 8]
but in Mathematica 7.0.1 (tested on Windows and Linux) it never completes and hogs a CPU indefinitely. Wolfram are aware of this one and it should be fixed in the next release. Thanks to Gábor Megyesi of Manchester University for sending me this one.
Feel free to let me know of others that you find but please bear in mind the points at the beginning of this post.
In order to write fully parallel programs in MATLAB you have a few choices but they are either hard work, expensive or both. For example you could
- Write parallel mex files using C and OpenMP
- Drop a load of cash on the parallel computing toolbox from the Mathworks
- Use the free parallel toolbox, pMATLAB
Wouldn’t it be nice if you could do no work at all and yet STILL get a speedup on a multicore machine? Well, you can….sometimes.
Slowly but surely, The Mathworks are parallelising some of the built in MATLAB functions to make use of modern multicore processors. So, for certain functions you will see a speed increase in your code when you move to a dual or quad core machine. But which functions?
On a recent train journey I trawled through all of the release notes in MATLAB and did my best to come up with a definitive list and the result is below.
Alongside each function is the version of MATLAB where it first became parallelised (if known). If there is any extra detail then I have included it in brackets (typically things like – ‘this function is only run in parallel for input arrays of more than 20,000 elements’). I am almost certainly missing some functions and details so if you know something that I don’t then please drop me a comment and I’ll add it to the list.
Of course when I came to write all of this up I did some googling and discovered that The Mathworks have already answered this question themselves! Oh well….I’ll publish my list anyway.
Update 11th May 2012 While optimising a user’s application, I discovered that the pinv function makes use of multicore processors so I’ve added it to the list. pinv makes use of svd which is probably the bit that’s multithreaded.
Update 18th February 2012: Added a few functions that I had missed earlier: erfcinv, rank,isfinite,lu and schur. Not sure when they became multithreaded so left the version number blank for now
Update 16th June 2011: Added new functions that became multicore aware in version 2011a plus a couple that have been multicore for a while but I just didn’t know about them!
Update 8th March 2010: Added new functions that became multicore aware in version 2010a. Also added multicore aware functions from the image processing toolbox.
abs (for double arrays > 200k elements),2007a acos (for double arrays > 20k elements),2007a acosh (for double arrays > 20k elements),2007a applylut,2009b (Image processing toolbox) asin (for double arrays > 20k elements),2007a asinh(for double arrays > 20k elements),2007a atan (for double arrays > 20k elements),2007a atand (for double arrays > 20k elements),2007a atanh (for double arrays > 20k elements),2007a backslash operator (A\b for double arrays > 40k elements),2007a bsxfun,2009b bwmorph,2010a (Image processing toolbox) bwpack,2009b (Image processing toolbox) bwunpack,2009b (Image processing toolbox) ceil (for double arrays > 200k elements),2007a conv,2011a conv2,(two input form),2010a cos (for double arrays > 20k elements),2007a cosh (for double arrays > 20k elements),2007a det (for double arrays > 40k elements),2007a edge,2010a (Image processing toolbox) eig erf,2009b erfc,2009b erfcinv erfcx,2009b erfinv,2009b exp (for double arrays > 20k elements),2007a expm (for double arrays > 40k elements),2007a fft,2009a fft2,2009a fftn,2009a filter,2009b fix (for double arrays > 200k elements),2007a floor (for double arrays > 200k elements),2007a gamma,2009b gammaln,2009b hess (for double arrays > 40k elements),2007a hypot (for double arrays > 200k elements),2007a ifft,2009a ifft2,2009a ifftn,2009a imabsdiff,2010a (Image processing toolbox) imadd,2010a (Image processing toolbox) imclose,2010a (Image processing toolbox) imdilate,2009b (Image processing toolbox) imdivide,2010a (Image processing toolbox) imerode,2009b (Image processing toolbox) immultiply,2010a (Image processing toolbox) imopen,2010a (Image processing toolbox) imreconstruct,2009b (Image processing toolbox) int16 (for double arrays > 200k elements),2007a int32 (for double arrays > 200k elements),2007a int8 (for double arrays > 200k elements),2007a inv (for double arrays > 40k elements),2007a iradon,2010a (Image processing toolbox) isfinite isinf (for double arrays > 200k elements),2007a isnan (for double arrays > 200k elements),2007a ldivide,2008a linsolve (for double arrays > 40k elements),2007a log,2008a log2,2008a logical (for double arrays > 200k elements),2007a lscov (for double arrays > 40k elements),2007a lu Matrix Multiply (X*Y - for double arrays > 40k elements),2007a Matrix Power (X^N - for double arrays > 40k elements),2007a max (for double arrays > 40k elements),2009a medfilt2,2010a (Image processing toolbox) min (for double arrays > 40k elements),2009a mldivide (for sparse matrix input),2009b mod (for double arrays > 200k elements),2007a pinv pow2 (for double arrays > 20k elements),2007a prod (for double arrays > 40k elements),2009a qr (for sparse matrix input),2009b qz,2011a rank rcond (for double arrays > 40k elements),2007a rdivide,2008a rem,2008a round (for double arrays > 200k elements),2007a schur sin (for double arrays > 20k elements),2007a sinh (for double arrays > 20k elements),2007a sort (for long matrices),2009b sqrt (for double arrays > 20k elements),2007a sum (for double arrays > 40k elements),2009a svd, tan (for double arrays > 20k elements),2007a tand (for double arrays > 200k elements),2007a tanh (for double arrays > 20k elements),2007a unwrap (for double arrays > 200k elements),2007a various operators such as x.^y (for double arrays > 20k elements),2007a Integer conversion and arithmetic,2010a
3435 = 33 + 44 + 33 + 55
Isn’t this a lovely little identity? Check out this paper by Daan van Berkel in the arXiv for the details.
Earlier today I was chatting to a lecturer over coffee about various mathematical packages that he might use for an upcoming Masters course (note – offer me food or drink and I’m happy to talk about pretty much anything). He was mainly interested in Mathematica and so we spent most of our time discussing that but it is part of my job to make sure that he considers all of the alternatives – both commercial and open source. The course he was planning on running (which I’ll keep to myself out of respect for his confidentiality) was definitely a good fit for Mathematica but I felt that SAGE might suite him nicely as well.
“Does it have nice, interactive functionality like Mathematica’s Manipulate function?” he asked
Oh yes! Here is a toy example that I coded up in about the same amount of time that it took to write the introductory paragraph above (but hopefully it has no mistakes). With just a bit of effort pretty much anyone can make fully interactive mathematical demonstrations using completely free software. For more examples of SAGE’s interactive functionality check out their wiki.

Here’s the code:
def ftermSquare(n):
return(1/n*sin(n*x*pi/3))
def ftermSawtooth(n):
return(1/n*sin(n*x*pi/3))
def ftermParabola(n):
return((-1)^n/n^2 * cos(n*x))
def fseriesSquare(n):
return(4/pi*sum(ftermSquare(i) for i in range (1,2*n,2)))
def fseriesSawtooth(n):
return(1/2-1/pi*sum(ftermSawtooth(i) for i in range (1,n)))
def fseriesParabola(n):
return(pi^2/3 + 4*sum(ftermParabola(i) for i in range(1,n)))
@interact
def plotFourier(n=slider(1, 30,1,10,'Number of terms')
,plotpoints=('Value of plot_points',[100,500,1000]),Function=['Saw Tooth','Square Wave','Periodic Parabola']):
if Function=='Saw Tooth':
show(plot(fseriesSawtooth(n),x,-6,6,plot_points=plotpoints))
if Function=='Square Wave':
show(plot(fseriesSquare(n),x,-6,6,plot_points=plotpoints))
if Function=='Periodic Parabola':
show(plot(fseriesParabola(n),x,-6,6,plot_points=plotpoints))
Within every field of human endeavor there is a collection of Holy Grail-like accomplishments; achievements so great that the attainment of any one of them would instantly guarantee a place in the history books. In Physics, for example, there is the discovery of the Higgs boson or room temperature superconductivity; Medicine has the cure for cancer and how to control the ageing process whereas Astronomy has dark matter and the discovery of extra-solar planets that are capable of supporting life.
Of course, mathematics is no exception and its Holy Grail set of exploits include problems such as the proof of the Riemann hypothesis, the Goldbach conjecture and the Collatz Problem. In the year 2000, The Clay Mathematics Institute chose seven of what it considered to be the most important unsolved problems in mathematics and offered $1 million for the solution of any one of them. These problems have since been referred to as The Millenium Prize Problems and many mathematicians thought that it would take several decades before even one was solved.
Just three years later, Grigori Perelman solved the first of them – The Poincaré conjecture. Stated over 100 years ago (in 1904 to be exact) by Henri Poincaré, the conjecture says that ‘Every simply connected closed three-manifold is homeomorphic to the three-sphere’. If, like me, you struggle to understand what that actually means then an alternative statement provided by Wolfram Alpha might help – ‘The three-sphere is the only type of bounded three-dimensional space possible that contains no holes.’ 99 years later, after generations of mathematicians tried and failed to prove this statement, Perelman published a proof on the Internet that has since been verified as correct by several teams of mathematicians. For this work he was awarded the Field’s Medal, one of the highest awards in mathematics, which he refused. According to Wolfram Alpha, Perelman also refused the $1 million from the Clay Institute but, as far as I know at least, he has not yet been offered it (can anyone shed light on this matter?).
Yep, Girgori Perelman is clearly rather different from most of us. Not only is he obviously one of the most gifted mathematicians in the world but he also sees awards such as the Field’s Medal very differently from many of us (after all, would YOU refuse such an award – I know I wouldn’t!). So, what kind of a man is he? How did he become so good at mathematics and why did he turn down such prestigious prizes?
In her book, Perfect Rigor, Masha Gessen attempts to answer these questions and more besides by writing a biography of Perelman. Starting before he was even born, Gessen tells Perelman’s story in the words of those who know him best – his friends, colleagues and competitors. Unfortunately, we never get to hear from the man himself because he cut off all communications with journalists before Gessen started researching the book. Despite this handicap, I think that she has done an admirable job and by the end of it I have a feeling that I understand Perelman and his motives a little better than before.
This is not a book about mathematics, it is a book about people who DO mathematics and gives an insight into the pressures, joys and politics that surround the subject along with what it was like to be a Jewish mathematician in Soviet-era Russia. What’s more, it is absolutely fascinating and I devoured it in just a few commutes to and from work. With hardly an equation in sight, you don’t need pencil and paper to follow the story (unlike many of the books I read on mathematics), all you need is a few hours and somewhere to relax.
The only problem I have with this book is that by the end of it I didn’t feel like I knew much more about the Poincaré conjecture itself despite getting to know its conqueror a whole lot more. Since I didn’t know much (Oh Ok…anything) about it to start with this is a bit of a shame. Near the end of writing this review, I took a look at what reviewers on Amazon.com thought of it and it seems that some of them are also disappointed at the mathematical content of the book and they come from a position of some authority on the subject. The best I can say is that if you want to learn about the Poincaré conjecture then this probably isn’t the book for you.
If, on the other hand, you want to learn more about the human being who slayed one of the most difficult mathematical problems of the millennium then I recommend this book wholeheartedly.
The carnival is back and it’s better than ever!
The 59th Carnival of Math has been published by Jason Dyer over at Number Warrior and is truly epic! The range of topics on offer is astonishing including mathematical clocks, ants on rubber bands, an entire quiz on the number zero, the game of life, cheating the derivatives market and whether or not an omnipotent being can create a rock so heavy that He/She cannot lift it?
The next carnival (the 60th) is set to be published on Friday December 4th but currently has no host set. If you are a math blogger and would like to get involved then drop me a comment and let me know. Hosting a carnival is not difficult and is a great way to get involved with the wider mathematics blogging community. As a bonus, it will help get your blog a lot of free publicity!
Ideally, I’m looking for someone who has never hosted a carnival before but old hands are welcome to volunteer too.
If you simply can’t wait for December’s Carnival of Maths then you can get your fix of community mathematical goodness from the next Math Teachers at Play Carnvial. Set to be hosted on 20th November by Denise of Let’s Play Math, the MTAP carnival focuses on preK-12 mathematics but, despite its name, it isn’t just for math teachers – anyone can join in.
Update (9th November 2009): The quest for the next carnival host is over. The 60th edition of the Carnival of Math will be hosted on Friday December 4th over at Sumidiot. Start getting your submissions in now and help make this the best carnival ever.
I’ve just installed Ubuntu version 9.10 (Karmic Koala) from scratch on my new work machine and noticed that you can no longer right click on a file to encrypt it. The functionality is still there – it just isn’t available by default. To get it just install the seahorse-plugins package as follows
sudo apt-get install seahorse-plugins
I did a reboot to get the changes to take but there is probably a less drastic way of getting the job done.

