Archive for July, 2021
Just over 4 years ago I was very happy with the 1.2 Teraflops of single precision performance I measured on my then-new Dell XPS 95600 laptop using MATLAB’s GPU Bench and noted that its performance was on-par with the first supercomputer I supported professionally. Double precision performance stank of course but I had gotten used to that with laptop GPUs!
Fast forward to 2021 and my personal computational landscape has changed substantially. The pandemic has confined me to my home office and high performance laptops don’t have quite the same allure that they did when I was doing most of my interesting computational work in airports and coffee shops. I swapped a 15 inch screen for a 49 inch Ultrawide monitor and my laptop is gathering dust while I enjoy my new Dell desktop with an 8 core Intel i7-11700 and an NVIDIA GTX 3070.
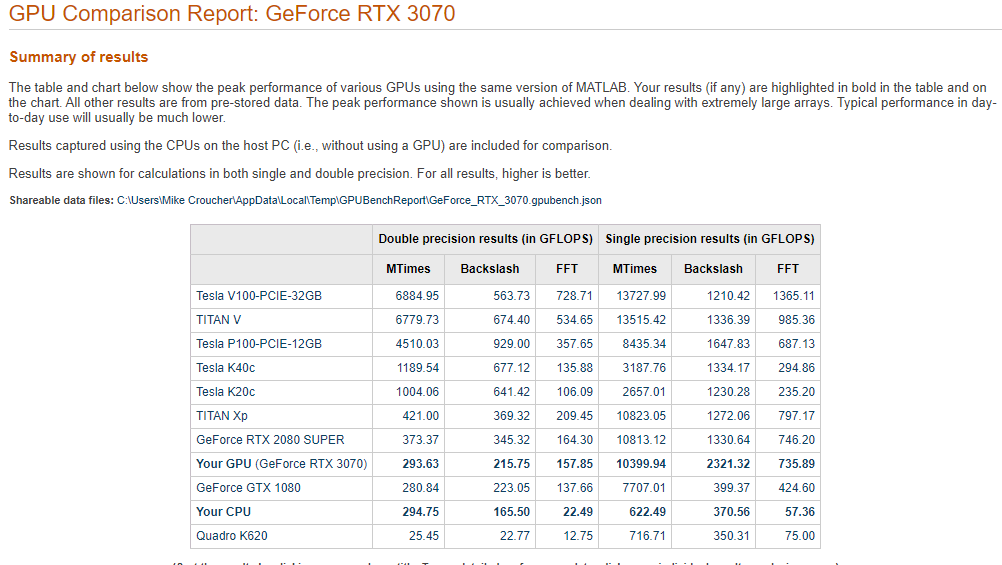
This is the first desktop machine I’ve personally owned for almost two decades and the amount of performance I got for less money than the high spec laptops I used to favour is astonishing! Here are the GPU Bench results using MATLAB 2021a
The standout figure is 10,399 Gigaflops for single precision Matrix-Matrix multiplication. At only slightly shy of 10.4 Teraflops that’s almost an order of magnitude faster than the results that impressed me on my laptop 4 years ago!
Double precision performance is nothing to write home about but it never is on consumer NVIDIA GPU cards. I stopped being upset about that years ago!
The other result I find interesting with respect to my personal history of devices is the 622 Gigaflops result for single precision from the Intel i7 CPU. This is getting on for twice as fast as the GPU on my 2015 Apple MacbookPro which managed 349 Gigaflops….a machine I still use today although primarily for Netflix.
Welcome to the 194th Carnival of Mathematics! I am extremely late in posting this…so late in fact that the 195th edition as already been published!
194 has a few interesting properties. According to its wikipedia entry, 194 is an odious number that is also the smallest Markov number that is neither a Fibonacci number nor a Pell number. It’s the smallest number that can be written as the sum of three squares in five ways and is the number of irreducible representations of the Monster group.
Micro Visual Proofs – Animated proofs without words
Proofs without words have been around for a long time. Diagrams that demonstrate that a mathematical statement is ‘obviously’ true. The example that always springs to my mind is the one below that demonstrates that the sum of consecutive odd numbers is a square number.

Such things have appeared in print for years. The books by Nelsen are a wonderful source of many of them and the Mathematical Association of America has a few very nice interactive examples.
Tom Edgar has been working on videos that animate proofs without words for a new YouTube channel called Micro Visual Proofs and submitted the one below for this month’s Carnival of math.
2.648102… Has anyone seen this constant?
Peter Cameron has been working on graphs on groups and has come across the constant 2.648102…. In this post he discusses how it turned up and asks if anyone else has come across it. There’s an interesting discussion in the comments section
Electrostatics and the Gauss–Lucas Theorem
Insight into mathematical theorems can come from many different places with physics being an extremely common one! Physical problems can be very useful in making even the most abstract concepts more concrete. John Carlos-Baez demonstrates this perfectly in his post Electrostatics and the Gauss-Lucas Theorem
Mathematics from TikTok
When the carnival of mathematics first began, it was all about mathematical blogs – a medium that was relatively new at the time. There was something wonderful about seeing mathematicians, scientists, teachers and hobbyists communicating more directly with the world. Internet time moves quickly and there has since been an explosion of interesting mathematical discussion on many other social media platforms — one of these being TikTok.
In this twitter post by Howie Hua, a teacher of math to future elementary school teachers, Howie advertises a TikTok video where he asks ‘What Happens if we add fractions across?’
New TikTok video: What happens if we add fractions across? pic.twitter.com/RDfU7AHYKL
— Howie Hua (@howie_hua) May 21, 2021
The Mathematigals Show
Mathematigals is a new YouTube channel that asks explores things like ‘What do broccoli and lightning have in common?’ and The Potato Paradox. In this month’s submission they discuss the source of many a mathematical argument, The Monty Hall Problem. Head over to YouTube to subscribe to their channel and show your support.
21-card trick explained
Mathematics is at the foundation of many card tricks and here is Ganit Charcha demonstrating one of them
.
Ganit has several videos on various aspects of mathematics and you can subscribe to his channel to show your support.
Shock Me Amadeus
Larissa Fedunik-Hofman of Sydney’s Mathematical Research Institute writes:
“In this profile video of applied mathematician Bronwyn Hajek from the University of South Australia, Hajek describes how she is motivated by the
quest to solve tricky, obscure, unsolved partial differential equations. Hajek will visit the Sydney Mathematical Research Institute in coming
months to collaborate on a project to apply Lie symmetry methods to model biological shocks.
I hope you like this video, which covers her upcoming project and some of the mathematical breakthroughs that Hajek has been involved with in recent years.”
Chalkdust – A magazine for the mathematically curious
Robin Whitty submitted this post that celebrates the launch of issue 13 of the Chalkdust magazine which focuses on John Conway, creator of the game of life, among many other things.