Archive for May, 2014
If you type
open foo.app
in a Mac terminal window, or alternatively, click on foo.app in Finder the application foo will be launched.
It turns out that foo.app is actually a directory which made me wonder ‘What determines what gets launched?’
If you look inside an .app folder, you will find a Contents folder. Inside this will be, among other things, a file called Info.plist. It is this file that determines what gets launched. For example, there is an entry in this file called CFBundleExecutable that determines the executable to be launched.
Thanks to Chris Beaumont for the link above.
This year sees the 50th anniversary of the UK’s Institute of Mathematics and its Applications (IMA). As part of the celebrations, the IMA has published a book called 50 Visions of Mathematics.
Edited by Sam Parc, the book contains 50 mini chapters covering many aspects of mathematics written for the general reader. Topics include subjects such as ‘Whats the use of a quadratic equation’, ‘The mathematics of obesity’, ‘A glass of bubbly’ and ‘Motorway Mathematics’. The full list can be found under the ‘Table of Contents’ tab at http://ukcatalogue.oup.com/product/9780198701811.do
The level of mathematics required to understand this book isn’t high at all which makes it suitable for anyone with even a passing interest in the subject.
Along with the 50 essays, there are also 50 full colour mathematical images with number 6 being contributed by yours truly — based on some Mathematica code I wrote a few years ago.
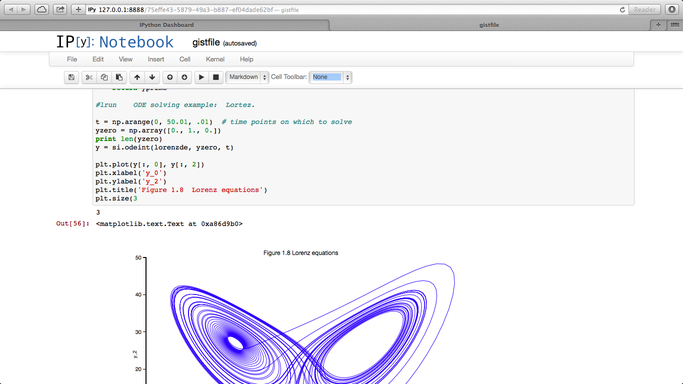
One of my favourite MATLAB books is The MATLAB Guide by Desmond and Nicholas Higham. The first chapter, called ‘A Brief Tutorial’ shows how various mathematical problems can be easily explored with MATLAB; things like continued fractions, random fibonacci sequences, fractals and collatz iterations.
Over at the SIAM blog, Don MacMillen, demonstrates how its now possible, trivial even, to rewrite the entire chapter as an IPython notebook with all MATLAB code replaced with Python.
The notebook is available as a gist and can be viewed statically on nbviewer.
What other examples of successful MATLAB->Python conversions have you found?
I’ve been a user and supporter of the commercial numerical libraries from NAG for several years now, using them in MATLAB, Fortran, C and Python among others. They recently updated their C library to version 24 which now includes 1516 functions apparently.
NAG’s routines are fast, accurate, extremely well supported and often based on cutting edge numerical research (I know this because academics at my University, The University of Manchester, is responsible for some of said research). I often use functions from the NAG C library in MATLAB mex routines in order to help speed up researcher’s code.
Here’s some of the new functionality in Mark 24. A full list of functions is available at http://www.nag.co.uk/numeric/CL/nagdoc_cl24/html/FRONTMATTER/manconts.html
• Hypergeometric function (1f1 and 2f1)
• Nearest Correlation Matrix
• Elementwise weighted nearest correlation matrix
• Wavelet Transforms & FFTs
—Three dimensional discrete single level and multi-level wavelet transforms
—Fast Fourier Transforms (FFTs) for two dimensional and three dimensional real data
• Matrix Functions
—Matrix square roots and general powers
—Matrix exponentials (Schur-Parlett)
—Fréchet Derivative
—Calculation of condition numbers
• Interpolation
— Interpolation for 5D and higher dimensions
• Optimization
— Local optimization: Non-negative least squares
—Global optimization: Multi-start versions of general nonlinear programming and least squares routines
• Random Number Generatorss
— Brownian bridge and random fields
• Statistics
— Gaussian mixture model
— Best subsets of given size (branch and bound )
— Vectorized probabilities and probability density functions of distributions
— Inhomogeneous time series analysis, moving averages
— Routines that combines two sums of squares matrices to allow large datasets to be summarised
• Data fitting
—Fit of 2D scattered data by two-stage approximation (suitable for large datasets)
• Quadrature
— 1D adaptive for badly-behaved integrals
• Sparse eigenproblem
— Driver for real general matrix, driver for banded complex eigenproblem
— Real and complex quadratic eigenvalue problems
• Sparse linear systems
— block diagonal pre-conditioners and solvers
• ODE solvers
— Threadsafe initial value ODE solvers
• Volatility
— Heston model with term structure
The IPython project started as a procrastination task for Fernando Perez during his PhD and is currently one of the most exciting and important pieces of software in computational science today. Last month, Fernando joined us at The University of Manchester after being invited by Nick Higham of the department of Mathematics under the auspices of the EPSRC Network Numerical Algorithms and High Performance Computing
While at Manchester, Fernando gave a couple of talks and we captured one of them using the University of Manchester Lecture Podcasting Service (itself based on a Python project). Check it out below.
This is a guest article written by friend and colleague, Ian Cottam. For part 1, see https://www.walkingrandomly.com/?p=5435
So why do computer scientists use (i != N) rather than the more common (i < N)?
When I said the former identifies “computer scientists” from others, I meant programmers who have been trained in the use of non-operational formal reasoning about their programs. It’s hard to describe that in a sentence or two, but it is the use of formal logic to construct-by-design and argue the correctness of programs or fragments of programs. It is non-operational because the meaning of a program fragment is derived (only) from the logical meaning of the statements of the programming language. Formal predicate logic is extended by extra rules that say what assignments, while loops, etc., mean in terms of logical proof rules for them.
A simple, and far from complete, example is what role the guard in a while/for loop condition in C takes.
for (i= 0; i != N; ++i) {
/* do stuff with a[i] */
}
without further thought (i.e. I just use the formal rule that says on loop termination the negation of the loop guard holds), I can now write:
for (i= 0; i != N; ++i) {
/* do stuff with a[i] */
}
/* Here: i == N */
which may well be key to reasoning that all N elements of the array have been processed (and no more). (As I said, lots of further formal details omitted.)
Consider the common form:
for (i= 0; i < N; ++i) {
/* do stuff with a[i] */
}
without further thought, I can now (only) assert:
for (i= 0; i < N; ++i) {
/* do stuff with a[i] */
}
/* Here: i >= N */
That is, I have to examine the loop to conclude the condition I really need in my reasoning: i==N.
Anyway, enough of logic! Let’s get operational again. Some programmers argue that i<N is more “robust” – in some, to me, strange sense – against errors. This belief is a nonsense and yet is widely held.
Let’s make a slip up in our code (for an example where the constant N is 9) in our initialisation of the loop variable i.
for (i= 10; i != N; ++i) {
/* do stuff with a[i] */
}
Clearly the body of my loop is entered, executed many many times and will quite likely crash the program. (In C we can’t really say what will happen as “undefined behaviour” means exactly that, but you get the picture.)
My program fragment breaks as close as possible to where I made the slip, greatly aiding me in finding it and making the fix required.
Now. . .the popular:
for (i= 10; i<N; ++i) {
/* do stuff with a[i]
}
Here, my slip up in starting i at 10 instead of 0 goes (locally) undetected, as the loop body is never executed. Millions of further statements might be executed before something goes wrong with the program. Worse, it may even not crash later but produce an answer you believe to be correct.
I find it fascinating that if you search the web for articles about this the i<N form is often strongly argued for on the grounds that it avoids a crash or undefined behaviour. Perhaps, like much of probability theory, this is one of those bits of programming theory that is far from intuitive.
Giants of programming theory, such as David Gries and Edsger Dijkstra, wrote all this up long ago. The most readable account (to me) came from Gries, building on Dijkstra’s work. I remember paying a lot of money for his book – The Science of Programming – back in 1981. It is now freely available online. See page 181 for his wording of the explanation above. The Science of Programming is an amazing book. It contains both challenging formal logic and also such pragmatic advice as “in languages that use the equal sign for assignment, use asymmetric layout to make such standout. In C we would write
var= expr;
rather than
var = expr; /* as most people again still do */
The visible signal I get from writing var= expr has stopped me from ever making the = for == mistake in C-like languages.
This is a guest article written by friend and colleague, Ian Cottam.
This brief guest piece for Walking Randomly was inspired by reading about some of the Hackday outputs at the recent SSI collaborative workshop CW14 held in Oxford. I wasn’t there, but I gather that some of the outputs from the day examined source code for various properties (perhaps a little tongue-in-cheek in some cases).
So, my also slightly tongue-in-cheek question is “Given a piece of source code written in a language with “while loops”: how do you know if the author is a computer scientist by education/training?”
I’ll use C as my language and note that “for loops” in C are basically syntactic sugar for while loops (allowing one to gather the initialisation, guard and increment parts neatly together). In other languages “for loops” are closer to Fortran’s original iterative “do loop”. Also, I will work with that subset of code fragments that obey traditional structured (one-entry, one-exit) programming constructs. If I didn’t, perhaps one could argue, as famously Dijkstra originally did, that the density of “goto” statements, even when spelt “break” or “continue”, etc., might be a deciding quality factor.
(Purely as an aside, I note that Linux (and related free/open source) contributors seem to use goto fairly freely as an exception case mechanism; and they might well have a justification. The density of gotos in Apple’s SSL code was illustrated recently by the so-called “goto fail” bug. See also Knuth’s famous article on this subject.)
In my own programming, I know from experience that if I use a goto, I find it so much more difficult to reason logically (and non-operationally) about my code that I avoid them. Whenever I have used a programming language without the goto statement, I have never missed it.
Now, finally to the point at hand, suppose one is processing the elements of an array of single dimension and of length N. The C convention is that the index goes from 0 to N-1. Code fragment A below is written by a non computer scientist, whereas B is.
/* Code fragment A */
for (i= 0; i < N; ++i) {
/* do stuff with a[i] */
}
/* Code fragment B */
for (i= 0; i != N; ++i) {
/* do stuff with a[i] */
}
The only difference is the loop’s guard: i<N versus i!=N.
As a computer scientist by training I would always write B; which would you write?
I would – and will in a follow-up – argue that B is better even though I am not saying that code fragment A is incorrect. Also in the follow-up I will acknowledge the computer scientist who first pointed this out – at least to me – some 33 years ago.