Archive for the ‘Carnival of Math’ Category
Welcome to the 90th edition of the Carnival of Mathematics and the first one hosted by me since I handed over the administrative reigns to the good people of aperiodical. The CoM is a great way to read about and promote mathematical blogging and has been running for over 5 years. Hosted on a different blog each month, it covers the entire mathematical spectrum from simple mucking around with numbers right up to cutting edge research.
Writers can submit their own posts for inclusion in a carnival if they like and anyone can submit any mathy post that they’ve found interesting– ideally, something written over the last month or so to keep it fresh.
If you want to keep up with the CoM, head over to its twitter feed or the dedicated page at aperiodical.
Trivia
Carnival tradition dictates that I post some trivia about this month’s edition number. Here’s what I came up with for 90:
- 90 is the only number that is the sum of its digits plus the squares of its digits (via NumberGossip)
- 90 is a Harshad number in base 10. It is also a Perrin Number, a pronic number, a unitary perfect number and a semi perfect number.
- 90 is the smallest number that has six representations as a sum of four positive squares (via Wolfram Alpha)
Neat Stuff
- Matthew Handy explains how researchers at MIT used geometric series to solve an economic problem in Zeno’s Facebook Page.
- Carnival regular, Pat Ballew tells us about a nice connection between numeric frieze patterns and triangulating polygons.
- Ethan Brown, a thirteen-year-old “Mathemagician” and the author of the blog coolmathstuff.com brings us Probability, The Number e, and Magic all in one
Computation
- The Numerical Algorithms Group (NAG) discusses Linear Quantile Regression, a new feature in the latest version of their software.
- Samir Kahn has been Modelling Flow Intertia in Three Couple Liquid Tanks using Maple.
- Cleve Moler, inventor of MATLAB, has written two posts on Conway’s Game of Life (part 1, part 2)
Puzzles and Games
- Shecky R brings us Mind Wrenching – A self-referential logic puzzle that will give your brain cells a workout.
- Brent Yorgey has been visualizing winning strategies for “nim-like” games and says ‘This is a post about visualizing winning strategies for certain games where players take turns removing counters from two piles. The games make for fun games to actually play, and analyzing them can get quite interesting!’
Funnies
- The xkcd comic shows how pointless the phrase ‘We are the fastest growing [whatever]‘ is
- Mark Dominus offers a koan on the Consistency of the Peano Axioms.
Art and Mathematics
- Egan Chernoff sent in Alternative Base Representation saying ‘I look forward to your critiques of my latest piece’
- Gianluigi Filippelli gives us Poincaré, Einstein and Picasso: children of time and says ‘Following an article by Arthur I. Miller on the Guardian, I try to tell the possible connections between cubism, mathematics and relativity.’
- Gianluigi continues his cultural theme with a look at some mathematical poems recently published in Nature in The day of mathematical poetry.
Books
- Shiva Kintali has reviewed a couple of books – Matching Theory by Laszlo Lovasz and Elements of Automata Theory by Jacques Sakarovitch.
Tricks and Tactics
- John D Cook gives us Binomial Coefficient Trick
Topology
- Mark Dominus of The Universe of Discourse gives us three posts this month: A two parter on topology and set theory (Click here for part 1 and here for part 2).
Teaching
- Dan McQuillan gives us On Trigonometric Nostalgia and says ‘This is a post about fostering a problem-solving mentality in a world where we do not even understand how our own tools work. It superimposes our nostalgia for the world we used to know with our innate curiosity, which still exists. Basic trigonometry is still fun and still relevant. Indeed, one can always ask questions and calculate!’
- Frederick Koh takes on the dot product in Understanding MATTERS (7) saying ‘This dot product concept involving parallel vector planes is rather fundamental, yet a handful of my students are unable to figure out how things exactly work. Hence I have decided to pen this detailed explanation in the hope that it will benefit not just my charges, but other math learners as well.’
- Augustus Van Dusen has written the first in an upcoming series of posts that will prove properties of logarthmic and exponential functions. Augustus says ‘This particular post will focus on the properties of logarithmic functions of real variables. Students in advanced placement calculus in high school and beginning college students who are not math majors are the intended audience.’
Comment
- Peter Rowlett asks does mathematics have a culture of historical inaccuracy?
- Mike Thayer submitted his article Tired of playing defense saying ‘These are my thoughts on the Andrew Hacker NY Times article from July, and the Roger Schank Washington Post article from earlier this week.It is my defense of teaching algebra…’
- Egan Chernoff submits Bill, you had me at “arithmetic” and asks ‘how do other people feel about the phrase “let’s do the math.” ‘
Not the only game in town
The Carnival of Mathematics isn’t the only mathematical blog carnival that’s doing the tour. There’s also the fantastic monthly Math Teachers at Play.
End
That’s it for the 90th Edition. Past editions written by me include 80, 76, 74 and 73 among others. For future editions keep an eye on @carnivalofmath and aperiodical.com
I’m hosting the 90th Carnival of Mathematics very soon. If you have written (or read) a mathematics blog article over the last month and want to give it more attention, why not make a submission? The deadline for submissions is 10th September.
For the last two years or so I have been doing the administration for The Carnival of Mathematics (CoM) and have had a lot of fun doing so. I first took over for carnival 59 (written by Jason Dyer and hosted over at NumberWarrior) and did the admin right up until number 84 which was published back in December 2011 by Guillermo Bautista (see here and here for some history).
Recently, however, I have struggled to find the time to give the CoM the attention it deserves and so it is time to hand over the baton. Thankfully, some very able hands have taken it from me and I am happy to announce that Peter Rowlett, Katie Steckles and Christian Perfect will be taking care of business from now on. Submissions for Carnival 85 are already open.
I’ll still be around, blogging as usual here at WalkingRandomly and hosting the occasional Carnival myself but the carnival is now being cared for by the next generation. Submit something and give them a great welcome.
Welcome to the heavily delayed 80th Carnival of Mathematics. Apparently, 80 is the smallest number with exactly 7 representations as a sum of three distinct primes. Head over to Wolfram Alpha to find them. 80 is also the smallest number that is diminished by taking its sum of letters (writing out its English name and adding the letters using a=1, b=2, c=3, …) – EIGHTY = 5+9+7+8+20+25 = 74 (Thanks Number Gossip).
Over at The Endeavour, John Cook discusses the principle of the single big jump (complete with SAGE notebooks) where he demonstrates that ‘your total progress is about as good as the progress on your best shot’…but only if the distribution is right.
Denise asks “What was it really like to work and think in Roman numerals, and then to suddenly learn the new way of calculating? Find out with these new books about math history.” in Fibonacci Puzzle. She is also running a competition which will be ending very soon so you’ll need to hurry if you want to enter.
Guillermo Bautista discusses origami in Paper Folding: Locating the square root of a number on the number line while Gianluigi Filippelli explains how some researchers found a solution to a computational problem using a biological network.
David R. Wetzel gives us Saving the Sports Complex Algebra Project in an effort to better engage math students while Alexander Bogomolny brings us a whole host of engaging math activities for the summer break and Pat Ballew introduces a Sweet Geometry Challenge.
I came across a couple of interesting articles about Markov Chain Monte Carlo (MCMC) simulations this month. The first is from John Cook, Markov Chains don’t converge while the second is by Danny Tarlow, Testing Intuitions about Markov Chain Monte Carlo: Do I have a bug?
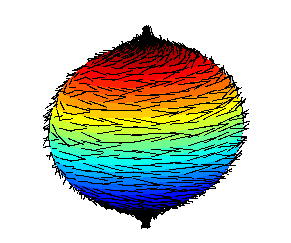
Matt Springer brings us Spherical Waves and the Hairy Ball Theorem (below)
Peter Rowlett of Travels in a Mathematical World fame recently had a paper published in Nature about the Unplanned Impact of Mathematics where he talks about how it can take decades, or even centuries, before research in pure mathematics can find applications in science and technology. For example, quaternions, a 19th century discovery which seemed to have no practical value, have turned out to be invaluable to the 21st century computer games industry! Something for the bean-counters to bear in mind when they obsess over short term impact factors of research.
Over at Futility Closet, we have a fun problem called School Reform.
Terence Tao gives us a geometric proof of the impossibility of angle trisection by straightedge and compass while the Geometry and the imagination blog discusses Rotation numbers and the Jankins-Neumann ziggurat.
Several people have been discussing recent changes in EPSRC (The UK’s main UK government agency for funding research and training in engineering and the physical sciences) including Timothy Gowers (A message from our sponsors), Burt Totaro (EPSRC dirigisme) and Paul Glendinning (Responding to EPSRC’s Shaping Capability Agenda).
Finally, one of my favourite mathematical websites is MathPuzzle.com. Written by Ed Pegg Jr, it is possibly the best online resource for recreational mathematics you can find. Go and take a look, you’ll be very glad you did.
That’s it for this month. The next Carnival of Math will be over at Wild About Math on 2nd September and you can submit articles using the carnival submission form. If you can’t wait until then, head over to I Hope This Old Train Breaks Down for the Math Teachers at Play carnival on August 19th. If you are new to the math carnivals and are wondering what’s going on then take a look at my introduction to mathematics carnivals.
Follow the Carnival of Math on Twitter: @Carnivalofmath This is also the best way of reaching me if you’d like to be a future host for the carnival.
I do the administration for the Carnival of Mathematics and am very happy to announce that the 77th edition has been published over at Jost a Mon. If you are unsure what a Math carnival is then check out my introductory article or just read some past editions from either the Carnival of Math itself or its sister publication, Math Teachers at Play which is run by Denis of Let’s Play Math fame.
The next Carnival of Math is scheduled to be hosted over at JimWilder.com and the submission form for articles is open now. If you’d like to host a future carnival of math on your blog or website then please contact me for further details.
Welcome to the very late 76th carnival of Maths. As per tradition, lets start with the trivia. 76 is an automorphic number , can be written as a sum of three squares (2^2+6^2+6^2) and is the 9th Lucas number.
Every now and then I get asked the question ‘Eigenvectors….so what are they good for?’ I’ve got a few stock answers but Language Log’s Mark Liberman goes the extra mile when he considers how they might have been used in Cinderella and goes on to discuss how they are used in linguistics. Are you suitably intrigued? Check it out in Eigenfeet, eigenfaces, eigenlinguistics, …
If you have worked on the classification of multivariate data then you may well have heard of or used the Mahalanobis distance (I came across it for the first time when working with MATLAB’s pdist function). It turns out that this commonly used metric has rather surprising origins! Read all about it in Anthropometry and Anglo-Indians over at Jost a Mon.
March 14th is, of course, Pi day and several bloggers have written something about everyone’s favouburite irrational number. Carnival regular, John D. Cook, brings us A Ramanujan series for calculating pi, 360 has The Difference and Qiaochu Yuan counters with Pi is still wrong. Finally, madkane brings us a Pi day limerick.
Over at God Plays Dice, Michael Lugo brings us A street-fighting approach to the variance of a hypergeometric random variable and some of Denise’s favourite math websites have gone AWOL over at Let’s Play Math. Can you help her find them?
Peter Rowlett asked Twitter for links to enthuse people about mathematics. Here are the answers. Finally, Guillermo Bautista gives us an example of the epsilon-delta definition of limits.
Your Carnival needs you
The Carnival of Math desperately needs people to write and host future editions. If you have a math related blog and would like a bucket-load of extra traffic then contact me for more information.
Welcome to the slightly delayed Carnival of Mathematics #74 – Tungsten Edition. In a departure from COM tradition, this edition is on the same blog as the last edition due to a lack of hosting volunteers. Fortunately, however, the volunteers are starting to turn up and so this is the last month that you’ll have to put up with me for a while. Next month will see the carnival hosted by Daniel over at General Musings and April will be taken care of by AcmeScience (thanks peeps!). The rest of the year is up for grabs so if you’d like to host a future carnival then contact me and we’ll work something out.
One tradition that I’m not about to give up on, however, is the number trivia section. So, let’s see what 74 has for us. In stark contrast to 73, the Chuck Norris of Numbers, 74 doesn’t seem to have much going for it. It’s probably overweight for a start since it is the 3rd hungry number (hungry because it tries to eat as much Pi as possible). Other than that it is odious, semiprime and altogether rather dull!
Enough of the trivia and on with the show.
First up we have a post from Datavisualization.ch which shows a set of infographics from around 150 years ago. Much of this work is rather beautiful and demonstrates that the field of infographics is much older than you might think.
For a rather more modern take on statistics and infographics I highly recommend the UK BBC Four TV documentary, The Joy of Stats. This was a one off show broadcast in late 2010 and hosted by Hans Rosling (Also the star of a brilliant TED talk). Several clips of the show are available over at The Open University and it was recently mentioned by The Royal Statistical Society.
From statistics and onto the theory of numbers with a post by Matt Springer called ‘Sunday Function’. In this post, Matt demonstrates a wonderfully simple proof concerning fractions which have terminating decimal expansions. It turns out that it just happened to be a Sunday morning when I read this delightful little post over coffee and it set me up for the day.
Number theory has been big news in the mathematical world recently thanks to some work by Ken Ono and colleagues who have found a finite, algebraic formula for partition numbers. The original papers can be found at http://www.aimath.org/news/partition/ (thanks to everyone on twitter who sent me that) and there has been discussion all over the web including at Wired.com and The Language of Bad Physics. Emory University (where Ken works) have a press-release but the best resource I’ve found so far is an informal talk by the man himself at YouTube (see below).
One of my biggest personal interests is mathematical software and so my contribution to this month’s carnival is a round-up of mathematical software news for January. January also saw a post from Wolfram Research on how to use some of Mathematica’s new control theory functions to stabilize an inverted pendulum which also serves as a nice introduction to some standard control theory techniques.
Another mathematical software article that was brought to my attention last month was a post from the Mathcad team concerning a very simple looking integral. Computers often do symbolic calculus using different techniques to human beings and this is occasionally reflected in the results. Check out the article for the details.
On a lighter note, we have Music is Math: Ten Songs about Mathematics from Dave Richeson of ‘Division by Zero’ fame. My favourite of the bunch is ‘A finite simple Group of Order 2′ (below) which I’ve some across before. The rest of them, however, are new to me and a lot of fun (and in a couple of cases, quite nice to listen to).
My boss used to be a research mathematician and is something of a pedant (In a good way Chris…in a good way). It seems that this is a trait he has in common with Peter Rowlett, author of Travels in a mathematical world, who has written a piece called Pedantry on Euler and Masts where he investigates the facts behind an old Euler story. There’s also some interesting discussion of the difficulty of presenting maths for the masses.
Whereas I do Random Walking, Sander Huisman does Random Hopping and in the process he comes up with some great looking pictures and interesting mathematics.
John D. Cook compares the iPhone to the method of least squares in When it works, it works really well, Ed4All shows us a mental arithmetic short cut for squares ending in five and Math-Frolic presents A Seemingly Impossible Task, That Isn’t.
Last but by no means least, Guillermo Bautista, organiser of the Math and Multimedia blog carnival, gives us an introduction to similarity while Alasdair’s Musings brings us A cute result relating to sums of cubes.
- Follow the Carnival of Math on Twitter: @Carnivalofmath
- Learn more about Math Carnivals: What is a math carnival?
73 is an awesome number. In fact, one could argue that it’s the Chuck Norris of numbers. Here’s why (courtesy of Wikipedia, and Number Gossip):
- The mirror of 73, the 21st prime number, 37, is the 12th prime number. The number 21 has factors 7 and 3.
- In binary, 73 is a palindrome – 1001001
- Of the 7 binary digits representing 73, there are 3 ones.
- Every positive integer is the sum of at most 73 sixth powers.
- In octal, 73 is a repdigit – 111
- Pi Day occurs on the 73rd day of the year (March 14) on non-leap years
- 73 is the largest integer with the property that all permutations of all its substrings are primes
- 73 is the largest two-digit Unholey prime: such primes do not have holes in their digits
- 73 is the smallest number (besides 1) which is one less than twice its reverse
- 73 is the alphanumeric value of the word NUMBER: 14 + 21 + 13 + 2 + 5 + 18 = 73
73 is also the edition number of this, the latest Carnival of Mathematics, to which I bid you welcome. On with the show.
First up we have a mathematical calendar for 2011 courtesy of Ron Doerfler which focuses on Lightning Calculations. I have written about Ron’s calendar before and highly recommend it to all.
The beginning of a new calendar year is an opportunity for all of us to sit back and take stock of everything that took place over the previous 12 months. As a result you’ll find retrospectives of all kinds scattered around the internet and on TV such as The Best Tech Products of 2010, TV’s 11 best Watercooler Moments of the Year and so on. Over at his blog, Wild About Math, Sol Lederman points us to a much more mathematical restrospective of the year 2010 by giving us a heads up about an awesome looking new book.
Next we have the 2011 Mathematics game from Denise of Let’s Play Math; the rules of which can be most simply stated as “Use the digits in the year 2011 to write mathematical expressions for the counting numbers 1 through 100.” Head over there to see more detailed rules, hints, tips, discussion and solutions found so far.
If all of that isn’t quite enough to sate your appetite for all things 2011 then I suggest that you take a look at Patrick Vennebush’s post entitled 2011 – Prime Time which inspired Brent Yorgey to follow up with Prime Time in Haskell. I wonder if 2012 will inspire such mathematical and computational outpourings?
In her post, Two Planes, Tanya Khovanova stumbled across a seemingly innocent looking question in an old edition of Mathematics Teacher which made her take a deep breath and exclaim ‘Ooh, boy!’. Check it out to see what all the fuss is about.
In Redefining Great Britain, GrrlScientist highlights some new research that describes a clever way to redefine and redraw geographical areas using telephone communication networks — it relies on statistics and computing power.
Sander Huisman has a crack at inventing his own fractal based upon the q-gamma function using Mathematica and a heap of computer time. The resulting fractal zoom looks great. He’s also produced a really neat animation of a hinged tesselation.
How do you abbreviate the word ‘Mathematics’? Some say ‘math’ others say ‘maths’ but which came first and which is the most popular? In his post, Math/Maths in Google Books Ngrams, Peter Rowlett uses Google Ngrams to sample millions of books in order to try and determine the answer to these and similar questions.
The trapezoidal rule for numerical integration has been in the news recently and so John Cook of The Endeavour shows us Three surprises with the trapezoid rule.
Imagine that we want to bet on an event with m >= 2 possible outcomes, and that there are n >= 2 bookmakers taking bets on those outcomes. Note that the odds are known at the time the bets are placed, i.e., we have fixed-odds betting instead of pari-mutuel betting. We would like to know how to allocate our (limited) money, i.e., how much to bet on each outcome at each bookmaker. As we cannot foresee the future, we would very much like to lock in risk-less profits. In other words, we would like to find arbitrage opportunities (aka: “arbs”). In his post, Fixed-Odds Betting Arbitrage, Rod Carvalho discusses how, given the (fixed) odds posted by n bookmakers, we can detect the existence of arbitrage opportunities.
PhD student, Gianluigi Filippelli, considers a problem from way back in the 13th century in his post Fibonacci, Bombelli and imaginary numbers. Personally, I’ve always loved some of the historical aspects of mathematics and hope to attend a good course on it some day.
Finally, we have a post from Guillermo Bautista called Chess and the Axiomatic Systems where he provides an intuitive introduction to the notion of axiomatic systems through chess rules.
That’s it for this time but if you still need more mathematical blogging then check out The 12 Math Carnivals of 2010 and don’t forget to submit your articles to the forthcoming Math Teachers at Play carnival.
Follow the Carnival of Math on Twitter: @Carnivalofmath
2010 was a great year for mathematical blogging and this was reflected in the monthly Carnivals of Mathematics. Here they are again in case you missed them.
- January – 61st Carnival at Walkingrandomly
- February – 62nd Carnvial at The Endeavour
- March – 63rd Carnival at Mathrecreation
- April – 64th Carnival at Teaching College Math
- May – 65th Carnival at Maxwell’s Demon
- June – 66th Carnival at Wild About Math
- July – 67th Carnival at Travels in a Mathematical World
- August – 68th Carnival at Plus Magazine
- September – 69th Carnival at JD2718
- October – 70th Carnival at General Musings
- November – 71st Carnival at Theorem of the Day
- December – 72nd Carnival at 360
The cycle will be starting again next week when the 73rd carnival gets published right here at Walking Randomly. What happens after that is up to you because I need volunteers to host future editions. If you are interested then get in touch via the comments section of this post, via twitter or by email.
Links
- What is a maths carnival?
- Math Carnival submission form
- Math Teachers at Play – The sister carnival to CoM
The 64th Carnival of mathematics has been posted over at Maria’s Teaching College Math blog and it is rather different from the norm. Posted as a mind map, it includes articles on a Murder Mystery project for logarithms, weightlifting for the brain, MATLAB, R, the mathematics behind a good night’s sleep and much more.
If you are new to math carnivals and are wondering what is going on then check out my introductory post here.
Other recent carnivals include:
- Math Teachers at Play #24 – posted at Let’s play Math
- Carnival of maths #63 – posted at Mathrecreation
- Math Teachers at Play #23 – posted at Mathrecreation
- Carnival of maths #62 – posted at The Endeavour