Archive for the ‘Wolfram Alpha’ Category
This is the third in an ongoing series of articles where I take a look at some of the mathematical applications available for iPad. Click here for part 1 and here for part 2. If you are the author of a mathematical iPad app that you’d like me to review then feel free to contact me. Also, if you use any mathematical iPad app regularly and think that its awesome then contact me and let me know why.
Wolfram Alpha and the Wolfram Course Assistants
At the time of writing, Wolfram Research have several iPad apps available including the following:
- Wolfram Alpha
- Wolfram Music Theory Course Assistant
- Wolfram Calculus Course Assistant
- Wolfram Algebra Course Assistant
- Wolfram Astronomy Course Assistant
- Wolfram Multivariable Calculus Course Assistant
All of these apps are interfaces to Wolfram Alpha, the fantastic computational engine that I fell in love with upon its release. Sadly, the apps themselves do not live up to the quality that I have come to expect from Wolfram Research and, as one iTunes reviewer put it, they are very thin-soup. In my opinion, the only one worth buying is the Wolfram Alpha app and even that is questionable since you could just access Wolfram Alpha directly (and for free) from your iPad web-browser. I’ll admit that the keyboard provided by the app is occasionally useful though.
The course assistants offer no additional content compared to the Wolfram Alpha app (or the website); they simply offer a menu driven way to generate search queries that are then sent to Wolfram Alpha. I would spend my money elsewhere if I were you.
slcalc – ‘Kazuo Nakazato’
In my original Math on the iPad article I focused on all singing, all dancing computer algebra apps but sometimes all you need is a good, old fashioned calculator. There are hundreds available on the appstore and slcalc is my current favourite. slcalc has got a long history for a mobile app since its first outing was on the Linux-based Sharp Zaurus back in 2003. The current iPad version is great and includes a long calculation history, the ability to use variables, arbitrary precision calculation (up to 256 digits), big buttons and a reasonable set of functions. You can even program it (and here are some example programs). All this for $1.99 (there is a more limited free version also). I guess my only minus point would be that the colour scheme is a bit..um…odd! Oh, and it can’t do complex arithmetic either but they are only minor things that detract from an otherwise great app.
Here are the iTunes links
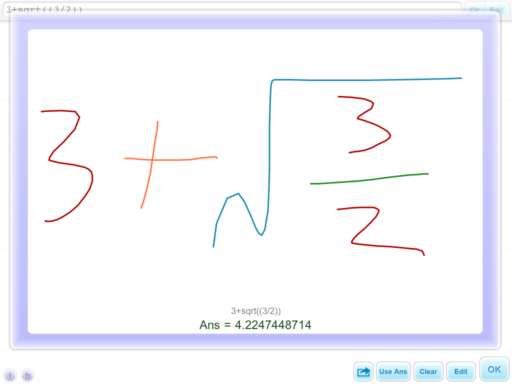
Handwriting Calculator – ‘Old Men’
The idea is brilliantly simple, you write the calculation that you want to perform directly onto your iPad’s screen and the iPad finds the result. No need to learn programming syntax or which button to press next, just write and calculate. Sadly, the reality isn’t quite so brilliant.
There are a limited number of functions (Basic arithmetic, square root, factorial and power) and the handwriting recognition is a bit flaky although I have to admit that my handwriting is probably more of a challenge than most. I also find myself wishing that I could use a stylus to write with since using my finger just doesn’t feel as precise. Furthermore, it turns out that I can punch numbers into a traditional calculator (such as slcalc above) MUCH faster than I can write them down.
In summary, its a nice idea and fun to play with for a couple of minutes but it just isn’t very useful and not worth the $1.99 asking price. iTunes link:
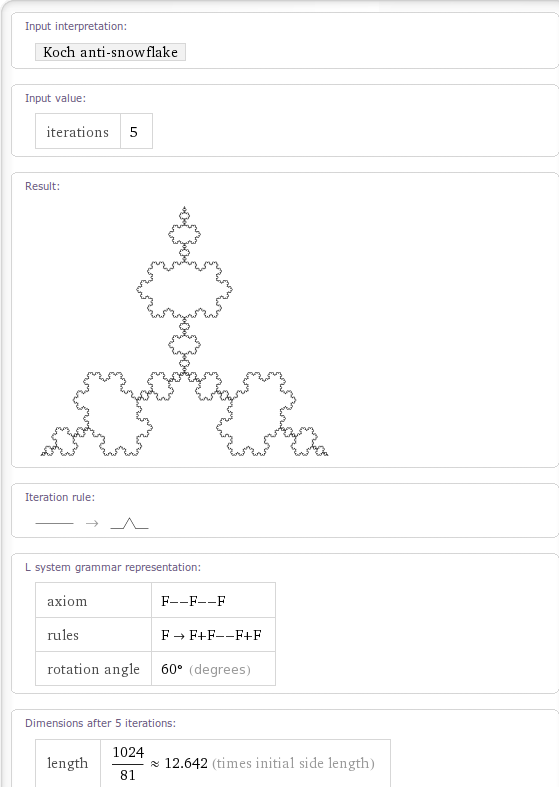
Back in May 2009, just after Wolfram Alpha was released, I had a look to see which fractals had been implemented. Even at that very early stage there were a lot of very nice fractals that Wolfram Alpha could generate but I managed to come up with a list of fractals that Wolfram Alpha appeared to know about but couldn’t actually render.
On a whim I recently revisited that list and am very pleased to note that every single one of them has now been fully implemented! Very nice.
Can you find any Wolfram Alpha fractals that I missed in the original post?
Someone recently emailed me to say that they thought Mathematica sucked because it couldn’t integrate abs(x) where abs stands for absolute value. The result he was expecting was
![]()
When you try to do this in Mathematica 7.0.1, it appears that it simply can’t do it. The command
Integrate[Abs[x], x]
just returns the integral unevaluated

I’ve come across this issue before and many people assume that Mathematica is just stupid…after all it appears that it can’t even do an integral expected of a high school student. Well, the issue is that Mathematica is not a high school student and it assumes that x is a complex variable. For complex x, this indefinite integral doesn’t have a solution!
So, let’s tell Mathematica that x is real
Integrate[Abs[x], x, Assumptions :> Element[x, Reals]]

which is Mathematica’s way of saying that the answer is -x^2/2 for x<=0 and x^2/2 otherwise, i.e. when x>0. It’s not quite in the form we were originally expecting but a moments thought should convince you that they are the same thing.
Interestingly, it seems that Wolfram Alpha guesses that you probably mean real x since it just evaluates the integral of abs(x) directly. It does, however, give the result in yet another form: in terms of the signum function, sgn(x):
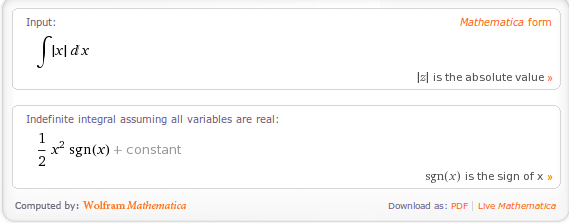
A couple of weeks ago I am pretty sure that Wolfram Alpha gave exactly the same result as Mathematica 7.0.1 so I wonder if they have quietly upgraded the back-end Kernel of Wolfram Alpha. Perhaps this is how Mathematica version 8 will evaluate this result?
I’m usually a big fan of Wolfram Research and their products but on reading the news that they had released a $50 iPhone app that hooked in to the Wolfram Alpha website I wondered if they had taken leave of their senses. Let’s see why…
Wolfram Alpha is a web service that is based on the extremely powerful computer algebra system, Mathematica, and it is very VERY cool. I won’t go into detail about what it can do here since many,many people have done that before (including me) but for the uninitiated think of it as a super-powerful graphical calculator that (partially) understands plain English and also has access to massive datasets from areas as diverse as the stock market, chemistry, popular music, language and physics.
Many students I know focus on the fact that it can eat their math homework for breakfast – not only giving the answer but also giving all of the steps that you’d need to get full marks on your coursework. Mathematics educators in the know are scrambling to come up with ways to harness this new freely available computational power while those not in the know are wondering why their students all get straight As in their coursework and yet flunk their exams.
All in all it’s very good stuff and you may be forgiven for thinking that it’s worth $50 for an app that can do all that. I would agree with you except for one, tiny little detail.
You can get all of this stuff for free! From Wolfram themselves!
Don’t believe me? OK, let’s prove it. Mashable have just reviewed the shiny new Wolfram iPhone app and have given it a big thumbs up because the reviewer has focused on all of the awesome features that Wolfram Alpha has. Choose any one of those nice examples shown in the mashable review – any one you like. Now, fire up your favourite web browser, head over to the Wolfram Alpha website and type in the exact same query.
Tell you what. I’ll do it for you. One of the examples given for the $50 app solves a simple differential equation – click on this link (from your iPhone if it suits you) to see exactly the same results for free.
I did exactly this on my Android phone and have included a screenshot for your delight and delectation (well, technically speaking I did it on the Android emulator since getting screenshots from an actual Android phone is tricky). The Wolfram Alpha query below cost me nothing:
I would have had to pay $50 to get this next one using the new iPhone app.

So, let’s be very clear here, Wolfram aren’t selling you an app that puts the power of Wolfram Alpha in your iPhone – they are just selling you a browser alternative that can only hit one website! For $50.
Of course they don’t JUST give you a browser alternative – according to the comments section over at mashable, the new alternative to the ‘I am Rich‘ app also gives you a more math-friendly onscreen keyboard and a query-history as well as formatting the results a little nicer than the built in browser.
Maybe that’s worth $50 to you but if so then you have a lot more money than me.
Update 2nd June 2010: As pointed out in the comments, Wolfram have since reduced the price of the Wolfram Alpha app significantly. At the time of writing it cost just £1.19 for iPhone and iPad versions of the software – now that’s more like it!
I stumbled across this website via one of my friend’s twitter feeds and it made me smile. Not everyone is impressed with Wolfram Alpha it seems :)
Up until now I have been using Wolfram Alpha as the ultimate geek toy and have been truly delighted with it but I thought it was high time I tried to consider how one might use it more seriously. So I set myself a task. Nothing too complicated you understand , after all I am still finding my feet with this new system, but something that may at least possibly come up in the real world. The task I set myself was
Obtain the actual data points for the Gross Domestic Product (GDP) of the UK from 1970 to 1980 inclusive. To allow me to import this data into pretty much every analysis program on the planet I’ll want it in a CSV file of the form
1970,GDP of UK for 1970 1971,GDP of UK for 1971 etc
Should be easy huh? Wolfram Alpha knows all about the GDP of the UK – if I Wolf GDP UK then I get the following output among other things).
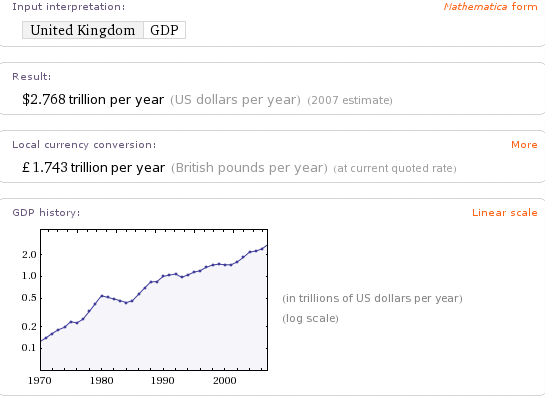
Fabulous! The data is clearly in there but how do I get it out in the form I want? Let’s try the hopeful UK GDP from 1970 to 1980. Alas I get the now familiar ‘Wolfram|Alpha isn’t sure what to do with your input.’ Moving on, I tried UK GDP 1970 to 1980 and UK GDP 1970-1980 but they didn’t work either.
I can get at a single datum easily enough. UK GDP 1970 gives me 123.7 billion for example but how do I get it to give me a list? Further experimentation showed me that I can get the GDP for any two years if I Wolf for something like (UK GDP 1970) (UK GDP 1971).
By now I feel I am getting somewhere. While playing with Wolfram Alpha (and reading the community forum) I’ve discovered that it will sometimes parse Mathematica code as well as plain English. ‘What I need‘, I thought, ‘is a piece of Mathematica code that would generate the query for me‘. So I tried
Table[“(GDP UK ” <> ToString[x] <> “)”, {x, 1970, 1980}]
but that didn’t work but then I shouldn’t be surprised because Table turns out to be one of the Mathematica functions that Wolfram Alpha doesn’t parse. Ho hum…
I tried a LOT of different inputs but the practical upshot is that the only one that worked was (UK GDP 1970) (UK GDP 1971) (UK GDP 1972) (UK GDP 1973) (UK GDP 1974) (UK GDP 1975) (UK GDP 1976) (UK GDP 1977) (UK GDP 1978) (UK GDP 1979) (UK GDP 1980). Lord help me if I wanted three times as many data points.
For the record I can get exactly what I wanted in Mathematica 7 with the following two lines of code and I worked out how to do it with a moments thought. Wolfram Alpha needs to be this easy!
data = Table[{x, CountryData["UK", {"GDP", x}]}, {x, 1970, 1980}];
Export["GDP.csv", data]
So, after some blood sweat and tears I had some actual numerical data but how could I export it to something useful. Wolfram Alpha always returns results as images by default.
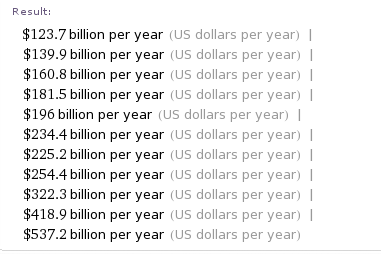
Which are not particularly useful if you want to do your own analysis. I can also get it as copyable plaintext and for this data set it looks like this
$123.7 billion per year (US dollars per year) | $139.9 billion per year (US dollars per year) | $160.8 billion per year (US dollars per year)| $181.5 billion per year (US dollars per year) | $196 billion per year (US dollars per year) | $234.4 billion per year (US dollars per year) | $225.2 billion per year (US dollars per year) | $254.4 billion per year (US dollars per year) | $322.3 billion per year (US dollars per year) | $418.9 billion per year (US dollars per year) | $537.2 billion per year (US dollars per year)
Hmmm. That’s going to need some pre-processing before I can import it into Excel I think – a job for a student or a Python script I think.
Now onto the Source information. It listed it’s primary sources as ‘Wolfram Alpha Curated data 2009’ and ‘Wolfram Mathematica CountryData’ with a shed load of Secondary sources such as ‘The US CIA WorldFactbook’. I have to say that I was a little surprised at this – how is Wolfram Alpha the Primary source of this data set? They must have got it from somewhere and THAT somewhere would be the primary source (or closer to it at least) IMHO.
In all honesty, I feel that putting itself as the primary source for data such as this is a bit like a student writing an essay and under ‘references‘ simply putting ‘My head‘.
Don’t get me wrong, I am starting to love Wolfram Alpha and think it’s got amazing potential but when you love someone you always want to see them do better for themselves. In this particular area I think that Wolfram needs to address the following
- Make it easier to get lists of data out of WA. Being able to parse Table[] might be a good start
- Allow export of tabular data in popular formats such as CSV and Excel.
- Work on the sources information a little. Wolfram Alpha didn’t actually generate this GDP data – they must have got it from somewhere and that should be listed as primary source.
Wolfram Alpha is a constantly moving target and it is quite possible that all of these issues will be addressed in no time (if Wolfram agrees that they are issues of course) so feel free to point out if any of the inputs I have linked to give different results from those stated here. I am also aware that I don’t know everything about this system so if I am being an idiot then feel free to point out how I should have phrased my query. Finally, if any new functionality comes online that makes all of this trivial then I would love to know.
Comments are, as always, welcomed.
An algebraic surface is a set of solutions to the general equation  f(x,y,z)=0 where f is a polynomial in the variables x,y and z. For example if you set f to the following polynomial
f(x,y,z)=0 where f is a polynomial in the variables x,y and z. For example if you set f to the following polynomial
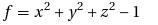
then the set of points x,y and z that satisfy  f(x,y,z)=0 forms a sphere of radius 1. You can get much more interesting surfaces than a sphere though. For example, set
f(x,y,z)=0 forms a sphere of radius 1. You can get much more interesting surfaces than a sphere though. For example, set
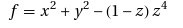
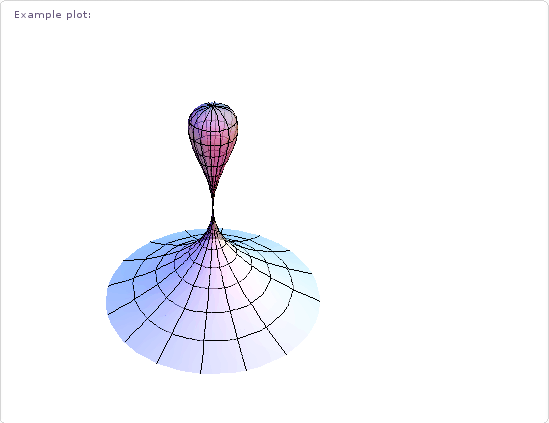
and you’ll get something known as the kiss surface – so called because the bottom section resembles a Hershey’s Kiss. Wolfram Alpha knows all about this surface and if you wolf Kiss Surface you’ll get a whole load of mathematical information about it along with the plot below.
One algebraic surface I have looked at in the past is the Heart Surface and it’s pretty obvious to see where it gets its name from.
At the time of writing, Wolfram Alpha knows about 129 different, named algebraic surfaces but for some of them it can be a little harder to work out how they got their name. Does anyone know why the one below is called the Flirt Surface for example?
Other interesting ones have names like Heaven and Hell,Citrus, Star and Plop!
This functionality is very nice indeed but for it to be really impressive I’d like to see a bit more (I wouldn’t be me if I didn’t want more). For example, it would be great if I could rotate each surface with the mouse – just as I can with 3D images in Mathematica. I’d also like to see more information on each surface such as how it got it’s name or the Mathematica code needed to produce the plot.
What’s your favourite algebraic surface and what extra functionality would you like to see in this area?
I apologise to any of my regular readers who may be tired of all of the Wolfram Alpha updates but I am pulling an all-nighter at the office and whenever I find myself waiting for my main computer to finish what it is doing, I end up feeding queries to Wolfram Alpha.
From the beginning, I knew that Wolfram Alpha knows about the calorie content of a lot of foods. If you walpha snickers bar for example you get quite a lot of information including the following.

OK, so you are on a diet and you’ve just given in and eaten a snickers bar. Now you have calorie guilt and you want to know how much you have to run to burn it all off and break even. Walpha the term exercise calories burned and you’ll get quite a large set of results including a set of editable input boxes similar to the screenshot below.

The input parameters refer to my run on the treadmill yesterday and I see that I burned 408 Calories according to Wolfram Alpha. Actually this is in complete agreement with the readout on the treadmill so whatever model they are using – they agree with each other. Put another way, my 5km run is worth almost one and a half snickers bars. On reflection, however, maybe I need to lay off the snickers bars because Wolfram alpha also tells me that my body mass index is a little on the high side. Ho hum….
What I find cool about these input boxes is that you can use any units you like. I used kilometers per hour but could have chosen miles per hour or a pace of 8 minutes per mile. Heck, I even put my height in parsecs and it just got on with the calculation. Wolfram Alpha also has a guess at how quickly I might run a marathon based on my current fitness using the Riegel and Cameron models. I’ve never run a marathon so couldn’t possibly comment on its accuracy.

Give or take a few hundred seconds I will be 1 billion seconds old on September 2nd 2009 and there will be a celebration :) Using Wolfram Alpha you can easily find out when you will be (or were) 1 billion seconds old simply by doing a query like
1 billion seconds from 18 May 2009
I’m going to have to try really hard to stop Walking Randomly from becoming a blog about Wolfram Alpha but I really am enjoying playing with this system.
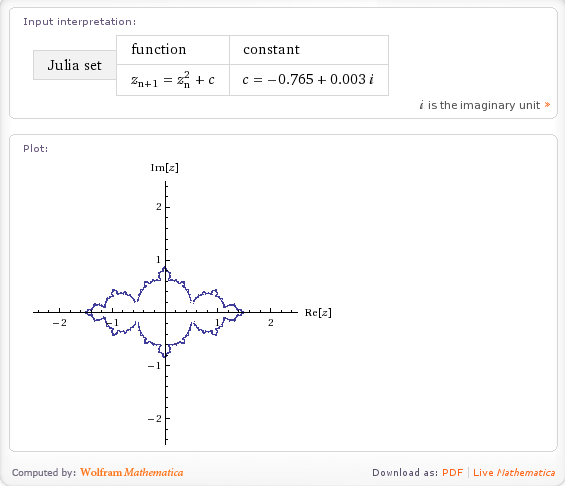
I saw a tweet from someone this morning which mentioned that you could plot the Julia Set using Wolfram Alpha. I had to try this for myself as soon as I could and, sure enough, you can plot the Julia set for any complex number Z: -0.765+0.003 I for example.
Very nice but what else can it do. If I Walpha fractals then I get the following output so I’d expect Wolfram Alpha to compute at least the Koch snow flake, the Sierpinski gasket, the Haferman carpet and the curlicue fractal and, sure enough, it does (click on the links to see for yourself)
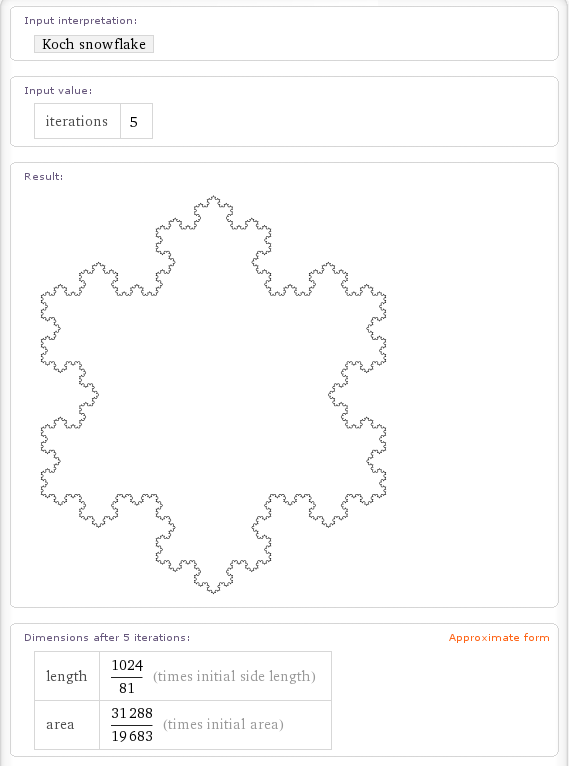
Here is a screenshot for the Koch Fractal.
These aren’t the only fractals it knows about though. If you walpha Pentaflake (a fractal close to my heart) then you get the following.
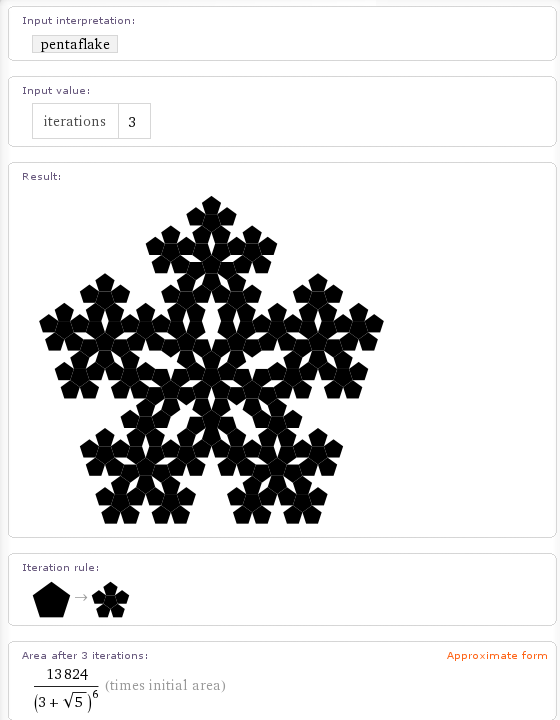
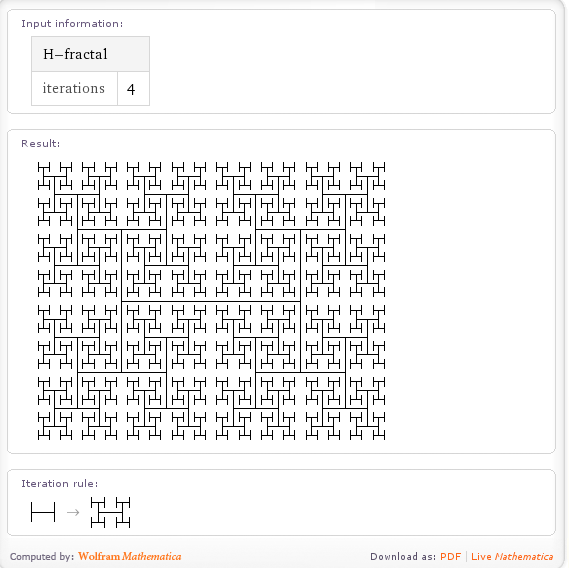
Wolfram Alpha can also calculate the H-Fractal.
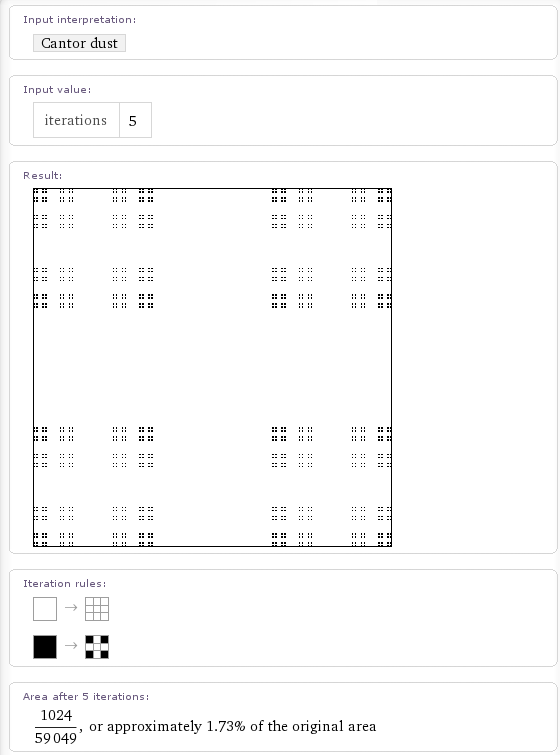
Cantor dust is in there too
as is the box fractal

It also looks like they are in the middle of implementing the Cesaro fractal. If you walpha the term then it tries to generate the fractal for a phase angle of pi/3 radians and 5 iterations. A few seconds later and the calculation times out. If you lower the number of iterations it returns a red box such as the one below. If my memory serves, Mathematica returns such a box if there is a problem with the graphics output. I hope to see this fixed soon.
Update:15th July 2009 – The Cesaro Fractal has now been fixed)
It also seems to know about the following fractals but doesn’t seem to calculate anything for them (yet). I say that it seems to know about them because it gives you an input field for ‘Iterations’ which implies that it knows that a number of iterations makes sense in this context. It’ll be cool to see all of these implemented in time.
(Note: None of these are implemented yet and may never be – I’ll update if that changes)
- Menger Sponge Update 21st December 2010 – this has now been implemented
- Gosper Island Update:15th July 2009 – this has now been implemented
- Apollonian Gasket Update 21st December 2010 – this has now been implemented
- Dragon Curve Update 21st December 2010 – this has now been implemented
- Hilbert Curve Update 21st December 2010 – this has now been implemented
- Peano curve Update 21st December 2010 – this has now been implemented
- Cantor Set Update:15th July 2009 – this has now been implemented
Some odd omissions (at the time of writing) are the Mandelbrot set (Update: 15th July 2009 – this has been done now) and the Lorenz attractor.
This is all seriously cool stuff for Fractal fans and shows the power of the Wolfram Alpha idea. Let me know if you discover any more Fractals that it knows about and I’ll add them here.
Update: I’ve found a few more computable fractals in Wolfram Alpha. Please forgive me for the lack of screenshots but this is getting to be a rather graphic-intensive post. The links will take you to a Wolfram Alpha query.