The Inverse Graphing Calculator
According to a new website, if you plot the following equation
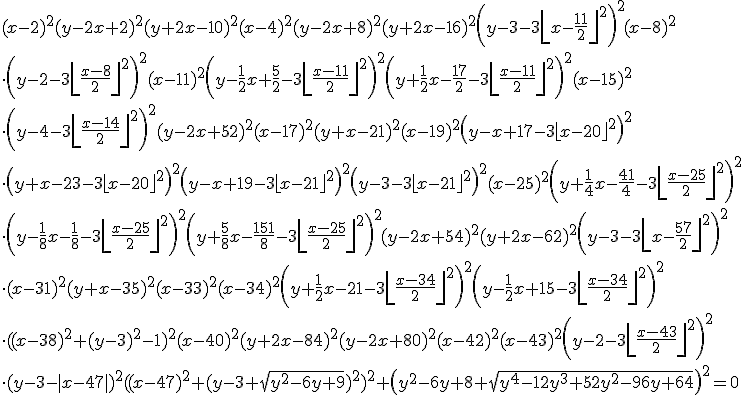
then you’ll get the following graph
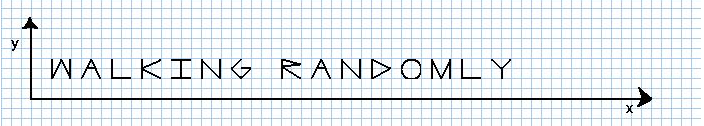
Head over to the Inverse Graphing Calculator to generate your own. It would be interesting to solve these equations and see if the website is correct.
If you liked this post then you may like this one too: Secret messages hidden inside equations

The simple “O” can’t be reproduced by WolframAlpha:
http://www.wolframalpha.com/input/?i=plot+%28%28x-3%29^2%2B%28y-3%29^2-1%29^2%2B%28y^2-6+y%2B8%2BSqrt%28y^4-12+y^3%2B52+y^2-96+y%2B64%29%29^2%3D0
Now what?
Yeah, looks like he’s right, though only tried it for single letters.
Right click the image, choose View Image (in Firefox), then you can copy the LaTeX from the address bar.
The functions are >= 0.
@vJD – it’s not as easy as that I’m afraid
@Szabolcs – I reproduced the two letters ‘ab’ in sequence by solving his equations using Mathematica. However, I may have made a mistake because my x axis appears to be rotated compared to his. I’ll post my code later today so others can play/comment.
If single letters work, then of course sequences will work too. The equations just need to be multiplied. I was lazy, so I just used ContourPlot, making the expression equal with a value slightly greater than 0 (and an increased MaxRecursion)
Admittedly ugly, but at least produces a more or less readable result:
e = ToExpression[
“(y-2x+2)^2(y+2x-10)^2\\left(\\left(y-3\\right)^2+\\left|x-\\frac{5}\
{2}\\right|+\\left|x-\\frac{7}{2}\\right|-1\\right)^2+\\left(y^2-6y+8+\
\\sqrt{y^4-12y^3+52y^2-96y+64}\\right)^2=0”, TeXForm]
ContourPlot[Log[First[e]] // Evaluate, {x, 2, 4}, {y, 1, 5},
MaxRecursion -> 3, AspectRatio -> Automatic]
Cool!