A little mathematics for Valentine’s day
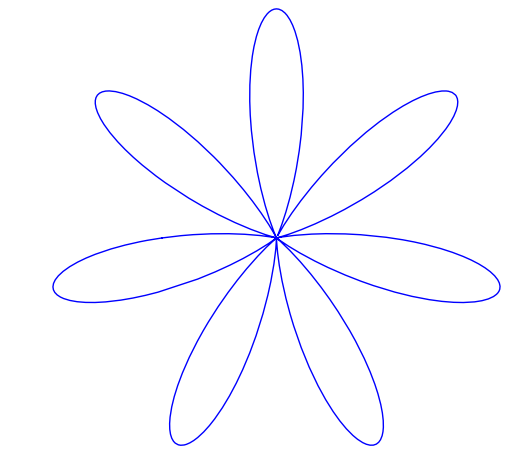
This is not a serious post but then mathematics doesn’t have to be serious all the time does it? Ever wondered what the equation of a 3D heart looks like? An old post of mine will help you find the answer using Mathematica. Click on the image for more details (and a demonstration that you can run using the free Mathematica player).
I don’t save all of my love for Mathematica though. I’ve got some for MATLAB too:
%code to plot a heart shape in MATLAB %set up mesh n=100; x=linspace(-3,3,n); y=linspace(-3,3,n); z=linspace(-3,3,n); [X,Y,Z]=ndgrid(x,y,z); %Compute function at every point in mesh F=320 * ((-X.^2 .* Z.^3 -9.*Y.^2.*Z.^3/80) + (X.^2 + 9.* Y.^2/4 + Z.^2-1).^3); %generate plot isosurface(F,0) view([-67.5 2]);
Did you know that the equation for a heart (or a cardioid if you want to get technical) is very similar to the equation for a flower? The polar equation you need is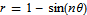 
and you get a rotated cardioid for n=1. Change n to 6 and you get a flower. Let’s use the free maths package, SAGE, this time.
First, define the function:
def eqn(x,n):
return(1-sin(n*x))
then plot it for n=1
polar_plot(eqn(x,1), (x,-pi, pi),aspect_ratio=1,axes=False)
and for n=7
polar_plot(eqn(x,7), (x,-pi, pi),aspect_ratio=1,axes=False)
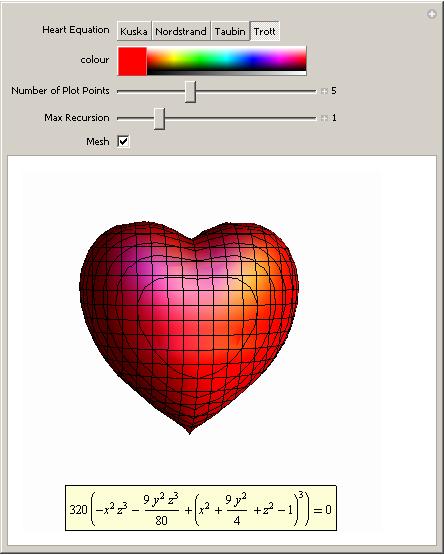
Back to Mathematica and the Wolfram Demonstrations project. We have a Valentine’s version of the traditional Tangram puzzle.
Feel free to let me know of any other Valentine’s math that you discover, puzzles, fractals or equations, it’s all good :)
Update Feb 14th 2011
Mariano Beguerisse Díaz sent me some MATLAB code that uses a variation on the standard mandelbrot and I turned it into the movie below. His original code is in the comments section
I have a ‘fuzzy’ Mandelbrot fractal in MATLAB
Just run this script, have a go!
% Fuzzy heart-shaped Mandelbrot fractal % Mariano Beguerisse % October 2010 % iterations n = 300; % resolution N = 200; % Create grid x = linspace(-1, 1, N); y = linspace(-1.4, .6, N); [X,Y] = meshgrid(x, y); Z = X + i*Y; Zn = Z; figure for j=1:n % Mandelbrot map with random noise Zn = -i*(Zn).^2 + (rand(N,N).^(1/5)).*Z; M = abs(Zn); ind1 = find(M<2); ind2 = find(M>=2); M(ind1) = 0; M(ind2) = -1; m = 1; imagesc(x, y, (M/m)) colormap([1 1 1; 1 0 0]) set(gca,'YDir','normal') title(n-j) pause(0.01) end title('Love or whatever', 'fontsize', 16)That’s nice :)