The unreasonable ineffectiveness of factoring
In his blog post, Factoring Schmactoring, Sam Shah took a look at how many quadratic equations of the form x^2+bx+c = 0 (where b and c are integers) could be factored over the integers and produced a chart that was a powerful reminder of just how few of these there are.
After reading his post I fired up Mathematica and set to work extending Sam’s original chart to include negative values of b and c – the result of which is shown below. Out of 441 different quadratic equations, only 76 have integer solutions which is only 17.23%, and yet these are the only ones that succumb to the heavily drilled and killed method of factoring.

Sam and his commentators discussed the serious question of whether or not we should even be teaching factoring these days (for the record, I think we should) but my concerns were much less lofty. I wondered if I’d make something pretty if I did a similar chart to the one above but for values of b and c ranging from -100 to 100.

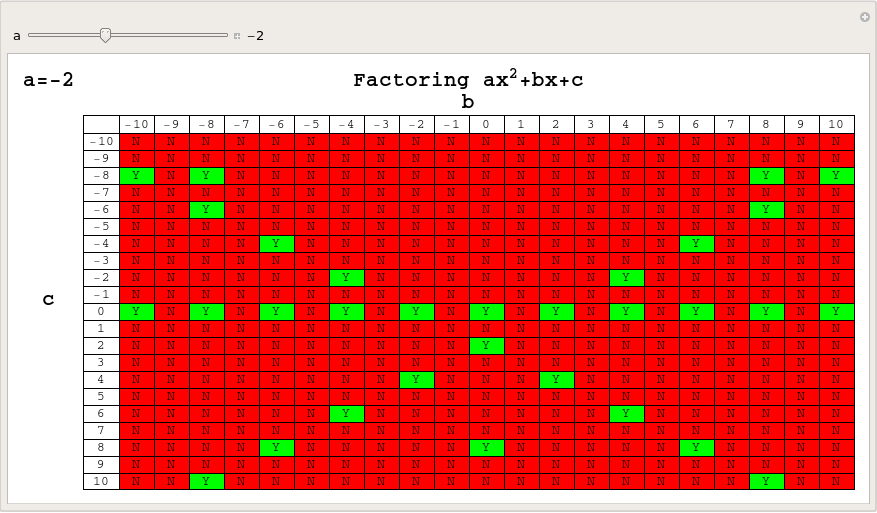
OK, so it’s not so pretty but it is possibly even more striking than the original charts – there is a LOT of red. Next, I wondered about values of a (the x^2 coefficient) other than 1 and thought that this was the perfect situation for a Manipulate (Click on the image to download an interactive version which can be used in either Mathematica or the free Mathematica Player):
Of course, when dealing with values of a other than one, we should include the possibility of rational solutions so let’s do that and assign rational solutions to the colour blue – again click on the image below for the Mathematica-Payer compatible interactive version.
I’m not really going anywhere with this – just having a bit of fun with Mathematica but comments are welcome.



really a great fun ,but didnt see any fascinating pattern in it, a little disappointing ,yes ?
:)
the third image is great,like something from the theory of cellular automata
Hi Wayne
Yes – a little disappointing that I didn’t find anything truly interesting but it doesn’t really matter. That’s the great thing about software like Mathematica or Maple – you can just play with ideas and it doesn’t take much time. It took me MUCH longer to write about this stuff than it did to do it.
AS for the 3rd image – I see what you mean. Personally it reminded me a little of User Defined Graphics as used by old 8-bit computers such as the Sinclair Spectrum.
Mike
I think the third image looks like a Christmas present tied up with a bow. Reminds me that it’s time to start my shopping…
It’s not surprising to me that factoring is of so little value in solving random equations. Similarly, if we could collect all the numbers and pull one out at random, we would not be likely to grab a rational one (or even a real number). But still, students need to start with the baby steps: learn to handle rational numbers, learn to understand and work with factors, etc.
And then, sometimes, it’s good for them (at least, for the best of them, lest they get too cocky) to be humbled by the overwhelming bloody red of the stuff that they don’t understand.
I think those images are pretty interesting indeed!
Look at the “slopes” of the green “lines” for the a=1 case. Especially in the -100 to 100 case you can see the slopes asymptotically approach infinity while the actual successful cases grow more sparse. At first I also considered looking at the angles between these “lines” but now I don’t think they share a common vertex. (maybe?)
However, they are forming an envelope of a quadratic. The green blocks seem to be the Integer Lattice Points of the tangent lines to the standard quadratic. (upside down since c is upside down)
The “a similar chart to the one above but for values of b and c ranging from -100 to 100” image is striking … given that the student is generally told to “find x” .
I see lots of x’s with different slopes…
Scott is quite right, and the images are interesting!
The quadratic X^2+bX+c factors over the integers precisely when it has integer roots. This means that there exists an integer n such that n^2+bn+c=0, or in other words c=-bn – n^2. These equations (c=-bn – n^2) define straight lines in the c-b plane – the “green lines” Scott mentions. So you can see that they do not share a common vertex: they intersect the b-axis at the perfect squares. And they are indeed the tangent to a lines to a quadratic, namely the quadratic c = (b^2)/4, whose lattice points correspond to the double root factorizations of our original quadratic X^2+bX+c; i.e. X^2+bX+((b^2)/4) = (X+(b/2))^2.