Walking Randomly

Welcome to the 58th Carnival of Maths – the late edition!  I should have published this a couple of days ago but work and life commitments got in the way and I have only now found time to put it together.  So, working on the assumption that late is better than never let’s get on with the show.

Whenever I discuss mathematics on this blog I often focus on using technology and so naturally I turned to technology to help me answer the traditional carnival question ‘What is interesting about the number n?‘ – where n is the edition number of the carnival being hosted.  So, let’s see what I can find out about the number 58 using the best technology the web can offer.

The Number Gossip website informs me that 58 is the smallest Smith number (in base 10) with a prime sum of digits. In addition (and more mundanely), 58 is also composite, deficient, even, evil and square free.  Wolfram Alpha also has a lot to say about the number 58 such as the fact that it is an idoneal number and that it can be expressed as the sum of two squares: 58= 3² + 7². Wolfram Alpha doesn’t finish there though since it also gives a wealth of other trivia about 58 such as how it can be written in binary, Roman Numerals, Greek, Babylonian and Mayan.  It tells us that its prime factorisation is 2*29, that 58 is the ASCII code for a colon along with the set of quadratic residues modulo 58.  Finally, it finishes off by telling us that

is a near integer.  A spot of googling helps me discover that  58 is the sum of the first seven prime numbers (2+3+5+7+11+13+17=58) and is also the sum of the totient function for the first thirteen integers .  Hmmm, fascinating!  However, enough of the number trivia and on with the show.

First up, we have a post from Jason Dyer of Number Warrior where he analyses one of his baby daughter’s favourite toys.  That’s right ladies and gentlemen, only 6 months old and already inspiring mathematics.

Brent Yorgey, of Math Less Travelled fame submits the post Challenge #12, Part II, where he discusses counting “hyperbinary” representations (like binary representations, but allowing up to two copies of each power of two instead of just one).  If you thought this carnival was late then you ain’t seen nothing yet ;)

Pat Ballew, author of the aptly titled Pat’s blog, sent in two related submissions for this edition of the carnival.  First up is a post about a problem and its solution in ‘problems from the land down under‘ (I don’t know about you but I can’t read that title without thinking of a certain song from the 80’s).   Pat worked on making the solution to this particular problem more understandable and, with a little help from his friends, he came up with a graphical solution.

The next submission comes from the blog Math with my kids where the writer asks some questions about sequences of rational numbers.  He knows the answers to four of the questions but the fifth question is open as far as he knows.

Moving over to The Endeavour, we have two related submissions from John D Cook all about The Mercator Projection and its inverse.

Finally, we have a submission from Paul Brabban who’s non-mathmo fiancee asked him ‘Why is a minus times a minus equal to a plus?’  How would you answer this question if asked?

And that’s pretty much it for this edition of the carnival – or at least I think it is.  I had to pull two of these submissions out of my spam bin so it seems that the filter has been a bit over-zealous recently.  I have published everything that was submitted to me so if you submitted something and it is not in this post then you have fallen foul of the spam filter gremlins. If you let me know via a comment to this post in the next few days then I’ll fix the situation.

Thanks to everyone who submitted.

The 58th Carnival of Maths will be hosted here on Friday 25th September and so I am looking for submissions.  Pretty much anything goes as long as it’s got something to with mathematics from advanced research through to the very basics.  The 57th carnival was hosted last week over at the blog 360 so head over there to see what it’s all about.

The carnival submission form no longer works but you can send your submissions in as comments to this post (I will supress them from publication to avoid spoiling the surprise), by email or send me a message on Twitter.  All I need is a link and a brief discussion about what the post is about – I’ll do the rest.

This isn’t the first time that the carnival has been hosted at Walking Randomly – I also hosted the 25th and 33rd editions so feel free to take a look at those too.

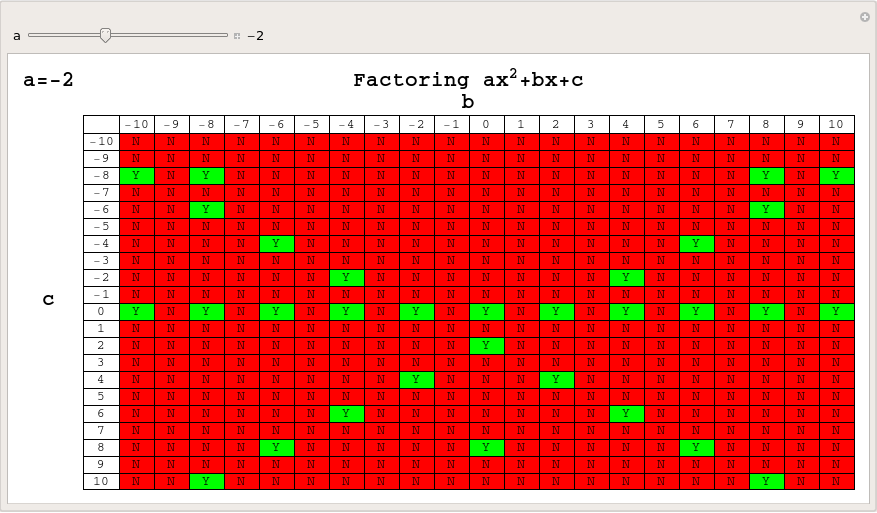
In his blog post, Factoring Schmactoring,  Sam Shah took a look at how many quadratic equations of the form x^2+bx+c = 0 (where b and c are integers) could be factored over the integers and produced a chart that was a powerful reminder of just how few of these there are.

After reading his post I fired up Mathematica and set to work extending Sam’s original chart to include negative values of b and c – the result of which is shown below.  Out of 441 different quadratic equations, only 76 have integer solutions which is only 17.23%, and yet these are the only ones that succumb to the heavily drilled and killed method of factoring.

Sam and his commentators discussed the serious question of whether or not we should even be teaching factoring these days (for the record, I think we should) but my concerns were much less lofty.  I wondered if I’d make something pretty if I did a similar chart to the one above but for values of b and c ranging from -100 to 100.

OK, so it’s not so pretty but it is possibly even more striking than the original charts – there is a LOT of red.  Next, I wondered about values of a (the x^2 coefficient) other than 1 and thought that this was the perfect situation for a Manipulate (Click on the image to download an interactive version which can be used in either Mathematica or the free Mathematica Player):

Of course, when dealing with values of a other than one, we should include the possibility of rational solutions so let’s do that and assign rational solutions to the colour blue – again click on the image below for the Mathematica-Payer compatible interactive version.

I’m not really going anywhere with this – just having a bit of fun with Mathematica but comments are welcome.

If you have learned how to program then the odds are that you have written a program that displays a list of prime numbers.  A prime number generator is a programming rite of passage that is almost up there with the ubiquitous ‘Hello World‘ application (for programmers who are going on to do numerical work at least).

There are various ways you might choose to do it but I bet that your first (or even your second or third) thought wouldn’t be ‘I know – I’ll use a regular expression‘. Someone known only as ‘Abigail’ obviously thought that the world desperately needed such a regex since he / she came up with the following incantation

^1?$|^(11+?)\1+$

Which is a regular expression that I assure you can be used to generate a list of all the prime numbers.  If you are in the mood for a puzzle then sit back, grab a cup of coffee and try to work out HOW it can generate the primes.

If you give up then head over to Python Programming for a full explanation along with Python code that demonstrates that it really does work.

Can anyone come up with regular expressions for other interesting series of numbers?

Update (27th August 2009): Someone pointed me to an alternative explanation here.

There are a lot of symbols in mathematics and I mean a LOT!  Not content with the entire Greek alphabet, mathematicians have gone on to use symbols from other alphabets such as Hebrew.  Once they had run out of alphabets they went on to invent hundreds of symbols themselves – a symbol for every occasion.

So, you are writing a paper in an esoteric (or maybe not so esoteric) area of mathematics and, naturally, you are writing it in Latex.   Suddenly you think to yourself ‘What’s the LaTeX command for <insert weird and wonderful glyph here>’

Searching in vain through list after list of LaTeX symbols you get to thinking ‘If only I could just draw the symbol and have the computer tell me what the LaTeX command is‘.

Well now you can!

Detexify is a new project from Philipp Kühl (who had the initial idea) and Daniel Kirsch (who implemented it) and is essentially an exercise in machine learning.  Sometimes it works perfectly (such as in the screenshot above) but other times it struggles a bit and you end up learning the commands for symbols you never even knew existed.

Teach the system

When it is struggling though, you can help it along.  Eventually you will find the symbol you were looking for and you can click on it to tell the system ‘That squiggle I drew – this is what I meant’ thus helping to train it for future searchers.

Other times though, you cannot blame it for not finding the symbol you meant.  For example I needed about 5 tries before I could get it to recognise my ham-fisted attempt at the lowercase zeta symbol.  This says a lot more about my poor handwriting and mouse skills than it does about the quality of Texify though.

Are you rubbish with the mouse?  Use your finger on your mobile phone then!

I found drawing even simple glyphs rather difficult with the mouse and soon found myself wishing that I could do it with my finger or a stylus so I was overjoyed to learn that Robin Baumgarten has released a version of Texify for Android mobile phones.  The Android app works exactly like the web version and connects to the server in order to do the actual recognition.

Iphone users haven’t been left out though since Daniel has released an app for that himself.

This is a great project that Daniel is now developing for his diploma thesis and you and you can read more about its progress over at his blog.

It never ceases to amaze me how researchers manage to find connections between the most seemingly disconnected of things.  A researcher at Manchester University, Bill Lionheart, conducts research into the mathematics of ‘seeing inside things with electricty’ and over at his blog he has a great story which basically says that a certain breed of fish are significantly better at this particular branch of mathematics than we are.

One particular quote I love is “Weakly electric fish are really interesting to us because they have the ability to solve a challenging mathematical problem when catching their food.” as it made me wonder how students would feel if they had to solve challenging mathematical problems in order to get their food :)

I’m a lucky guy!  I work for a major UK University and one of the perks of the job is that I (along with every other member of the University) get access to a massive array of academic journals and this is close to priceless as far as I am concerned.  I’d rather take a salary cut than lose that particular perk (shhhh, don’t mention this to my bosses) and I don’t even do any formal research!

I have been blogging for almost two years now and one thing I have learned from the whole experience is that the world contains legions of amateur scholars – people who do research for personal rather than professional reasons.  These scholars (and I like to think I am one of them) don’t want to publish papers or get qualifications, they simply want to learn about and discuss whatever subject takes their fancy.  In my case I focus on subjects such as mathematics and physics since they are (and always have been) the subjects that float my boat and they are also the subjects I studied both at school and at University.

Without having the journal access that I get via my employer I would find this hobby significantly more difficult and expensive to pursue.  Occasionally I get to see just how expensive it would be when I come across a journal which my University doesn’t have a subscription to.   One such journal is Physics Teacher and earlier today I wanted to get hold of a 2 page article published back in 1981 – almost 30 years ago.  The cost was $18.

$18 for two pages of work almost 3 decades old and I wasn’t even asking for it to be sent to me printed on gilt edged paper.  All I wanted was a pdf file which would cost almost nothing to send me.  For comparison, that $18 could get me one of several different maths books on my Amazon wish list.  If the journal had made it $5 or less then I wouldn’t be writing this – I would have just bought it.

I know that journals aren’t charities but surely this kind of asking price is simply too high.  If the work had only been published recently then I might be able to understand it – that $18 would go towards paying for editorial staff, peer review, publication etc but surely older articles aren’t worth this amount since all of their costs were covered years ago.

Why not learn from something like iTunes and make the cost of many articles so low that people don’t even stop to think if they want to spend the money or not?  If every article in Physics Teacher more than 25 years old only cost $1 then I (and probably many others) would buy lots of them and the journal would get a decent amount of cash.  Bandwidth is cheap so it wouldn’t really cost any more to send 20 files then it would to send 1 but I am a lot more likely to spend $20 on 20 files than $18 on 1.  Would it be better to charge the higher prices for the first 10 or 20 years from the publication date and then drop to $1 or so for older articles?

I’m not just picking on Physics Teacher though – many other journals seem to have a similar policy.  What do you think?  What would the best business model be?  Would you buy more journal articles if they only cost a dollar?

Take a wheel of radius 1 and set it rotating about its axis with a frequency of 1 turn per second. Attach a second wheel, of radius 1/2, to the circumference of the first and set this second wheel rotating about its axis at a frequency of 7 turns per second. Finally, attach a third wheel to the circumference of the second and set this wheel to rotate about it’s axis at a frequency of 17 turns per second.

Now, consider a point on the circumference of the third wheel. What pattern will it trace out as the three wheels rotate?  Click on the video below to find out.

I first came across this idea in a Wolfram demonstration by Daniel de Souza Carvalho.  Daniel’s demonstration focused on the fact that you could write down the equations of these curves in two different ways. If the wheels are rotating with frequencies a, b and c respectively then you can either describe the corresponding curve with a pair of parametric equations as follows:

or as a complex valued equation:

This was a nice demonstration but I wanted to see what sort of patterns I could get by changing the frequencies of the wheels. So, I downloaded Daniel’s demonstration, added some sliders and tick boxes and then uploaded the result. Wolfram Research cleaned up my code a bit and the result was published as the Wolfram Demonstration Wheels on Wheels on Wheels.

It turns out that you can get a LOT of different patterns out of this system as you can see below.

These systems were considered in the paper “Wheels on Wheels on Wheels—Surprising Symmetry,” Mathematics Magazine 69(3), 1996 pp. 185–189 by F. A. Farris. In this paper, Farris showed that the resulting curve exhibits m-fold symmetry if the three frequencies are congruent (mod m).

Can you think of any interesting variations to this system?

Update (6th July 2009): Taki has written another version of this demonstration which includes an animation of the wheels and also looked at an example with four wheels over at his blog, Mesh Mess.

Solution to problem of the week #6

Way back in April, I posed the following problem.  ‘Consider a square pyramidal pile of identical cannonballs of radius r such that the bottom layer contains 16 cannonballs (such as the pile in the diagram above). Find the volume (in terms of r) of the pyramid that envelops and contains the whole pile’

Since then I have received several answers (check out the comments section of the original post for a few of them) and all but one of them were wrong.  In my opinion, this is nothing to be too ashamed about since I couldn’t solve the problem either and I am not about to berate my readers for failing to do something that I couldn’t do myself!

So if I couldn’t do it then how did I know that all of these answers were incorrect?  Well clearly I had cheated and had access to a worked solution.  ‘My’ problem was in fact problem number 15 from one the 1840 undergraduate final exams at Cambridge University and a worked solution is given in the (now fully digitized, thanks to google) text Solutions for the Cambridge Problems 1840,1841.

The solution is

You’ll find the official worked solution to this problem on page 20 of ‘Solutions for the Cambridge Problems 180,1841’ (sadly, the diagram is missing) but James Graham-Eagle of the University of Massachusetts Lowell sent me not one but two different solutions in this pdf file and they are much easier to follow in my humble opinion.  Thanks for that James.

I’m glad that this problem wasn’t in my final exam!

A new math problem of the month series has started up over at problemas | teoremas – a dual language English, Portuguese blog written by Walking Randomly reader, Américo Tavares.  Américo successfully solved some of the problems I set here in the past and now he has started his own series.

Check out the first problem here but try not to look at the comments section if you don’t want any clues.