Archive for the ‘Wolfram Demonstrations’ Category

The Valentine’s Equations

February 14th, 2008

A couple of weeks ago I started thinking about Valentine’s day and, since I like equations that have interesting plots so much, I wondered if I could find one that had a heart-shaped graph. A quick google search came up Wolfram Research’s Heart Surface page.

The main page described a couple of heart shaped algebraic surfaces which looked nice but there were a few more on the Mathematica notebook that the page linked to. This notebook was rather old and included plots from old versions of Mathematica so on the train ride home I wrapped these equations in some Manipulate functions and sent the resulting demo to Wolfram. The result was published today on the Wolfram Demonstrations site.

heart demo

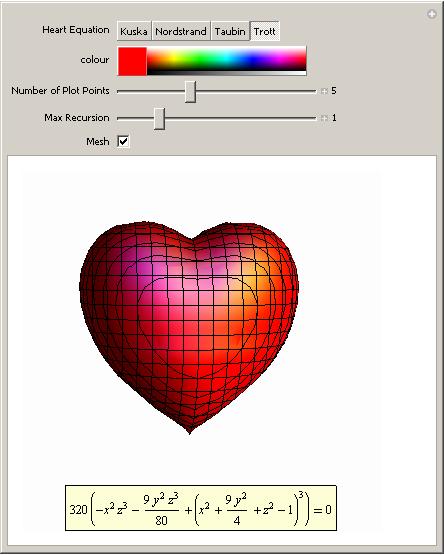
Essentially all this demo does is use Mathematica’s ContourPlot3D function to plot the curves formed from the following equations and allow you to play with the results a bit.

Nordstrand
\light -\frac{8}{45} x^2 z^3-y^2 z^3+\left(\frac{32 x^2}{9}+2 y^2+z^2-1\right)^3 = 0

Kuska

\light -\frac{1}{10} x^2 z^3-y^2 z^3+\left(2 x^2+y^2+z^2-1\right)^3=0

Taubin

\light -x^2 z^3-\frac{9 y^2 z^3}{80}+\left(x^2+\frac{9 y^2}{4}+z^2-1\right)^3=0

Trott

\light 320 \left(-x^2 z^3-\frac{9 y^2 z^3}{80}+\left(x^2+\frac{9 y^2}{4}+z^2-1\right)^3\right)=0

Each equation is named after the person who first wrote it down (to my knowledge at least). It’s a simple demo but I hope you like it.

Happy Valentine’s day.

5 comments

The Broken Heart Tangram

February 14th, 2008

I imagine that most of the people reading this will know what the Tangram puzzle is but just in case you are not one of them here is a quick excerpt from the Wikipedia page which says it all:

“Tangram (Chinese: 七巧板; pinyin: qī qiǎo bǎn; literally “seven boards of skill”) is a dissection puzzle. It consists of seven pieces, called tans, which fit together to form a shape of some sort. The objective is to form a specific shape with seven pieces. The shape has to contain all the pieces, which may not overlap. ”

The classical Tangram puzzle looks like this:

tangram

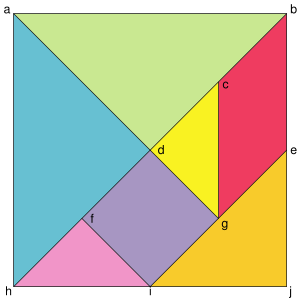
It is possible to make many shapes from these pieces; some of which are below (taken from tangrams.ca)

Tangram shapes

If you would like to have a go at making your own Tangram shapes then you can make your own Tangram set out of paper, buy a nice wooden one, try this java applet or use this Mathematica demonstration (written by Enrique Zeleny) using the free Mathplayer from Wolfram Research. There is even a Tangram game for the Nintendo DS!

In the week leading up to Valentine’s day I wondered if there is a standard variation of the classical Tangram puzzle that is constructed from a heart shape and I was delighted to discover that there is. Using Enrique’s Mathematica code as a starting point I wrote a demonstration called Broken Heart Tangram and it was published on the Wolfram Demonstrations site today.

heart tangram

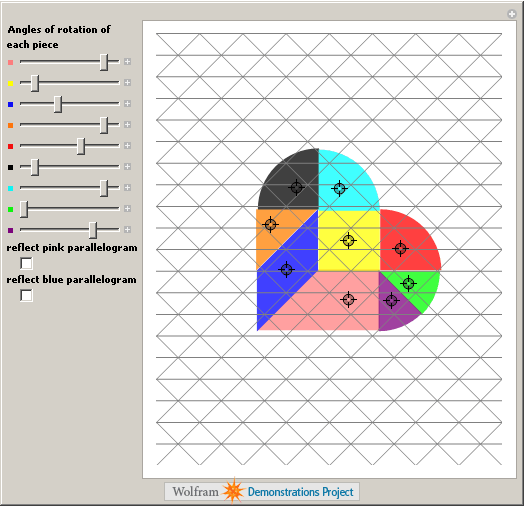
I hope you have fun with this demonstration and would love to see some of the shapes that you come up with. As always, comments are welcomed.

Other articles you may like

3 comments

The Polar Equations for Hearts and Flowers

February 14th, 2008

For my final Valentine’s day post I thought I would share a minor discovery I made while playing around with the polar equation

\light r=1-\sin(n\theta)

When n=1 the graph of this equation is a rotated cardioid which is exactly what I expected after reading the Math World page on the Heart Curve.

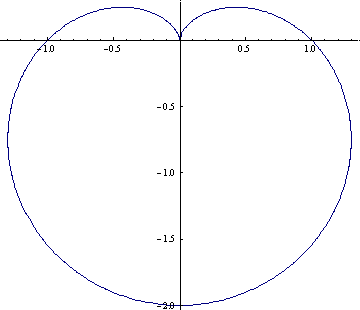
While playing around with the parameters I discovered that if you increase the value of n (to 10 say) then the resulting plot looks like a flower.

Very apt considering the time of year I think. If you would like to play with this equation yourself then feel free to try my very simple Wolfram Demonstration which was published today.

0 comments

Hello World – Mathematica Style

February 6th, 2008

A little while ago I discovered that if you plot the following equation over a certain range then the result is rather surprising.

\light f(x,y)=e^{-x^2-\frac{y^2}{2}} \cos (4 x)+e^{-3 \left((x+0.5)^2+\frac{y^2}{2}\right)}

A lot of people seemed to like this post and quite a few people reproduced the graph on their website so I thought I would revisit it. To allow people to play with this equation I have written a Wolfram Demonstration which was published yesterday; a screen shot is below.

 

Head over to Wolfram’s site in order to download it (and the source code if you wish). Remember you do not need to have a copy of Mathematica in order to run demonstrations such as this one – the free MathPlayer will do the job nicely.

0 comments