Problem of the week #6 – Cannonballs
Imagine that you were the Captain of a sailing ship a few hundred years ago and, in order to protect yourself from pirates, you had a few cannons. Cannons need cannonballs and it is well known that the best way to stack cannon balls is to arrange them as a square pyamid as in the image below.
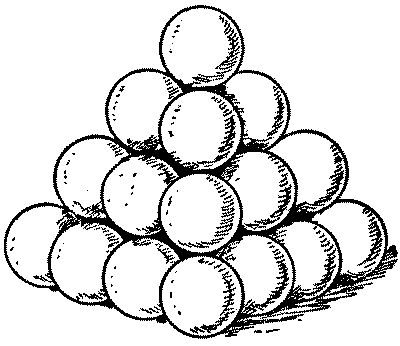
So, in this example you have 16 balls in the bottom layer, 9 balls in the next layer, then 4 and, finally, one at the top giving a total of 16+9+4+1 = 30 balls and we say that 30 is the 4th square pyramidal number. The first few such numbers are
- 1
- 5 (4+1)
- 14 (9+4+1)
- 30 (16+9+4+1)
- 55 (25+16+9+4+1)
Now, there is a well known problem called the Cannonball problem (Spolier alert: This link contains the solution) which asks ‘What is the smallest square number that is also square pyramidal number?’ but the traditional cannonball problem has been stated and solved by many people and so it isn’t my problem of the week.
My problem is as follows ‘Consider a square pyramidal pile of identical cannonballs of radius r such that the bottom layer contains 16 cannonballs (such as the pile in the diagram above). Find the volume (in terms of r) of the pyramid that envelops and contains the whole pile‘
As always, there are no prizes I’m afraid (but if you are a company who would like to sponsor prizes for future POTWs then let me know). I imagine that the solution to this will require a diagram so it might be best to put your solution on a pdf file, web page or some other visual media rather than using the comments section. Finding my email adress is yet another (easy) puzzle to solve.
Have fun.

hahaha, you should compete with blinkdagger.com or maybe join force with them.
We could discuss precisely what makes a stacking be “the best”, but I would say a face-centered cubic tetrahedral pyramid qualifies better for the title…
As for the problem, by looking at a cross section of the pyramid along a vertical plane passing through one of the base’s diagonals, I figured the pyramid we are looking for is halfway between one passing through the centers of the spheres in a 4×4 based pyramid, and one passing through the centers of the spheres in a 7×7 based pyramid. All things considered, the enveloping pyramid would have a 9r x 9r base, and a height of 9r√2/2, which yields a volume of 9³r³√2/6
Hi Jaime
It’s not the answer I’ve got. I guess the question is ‘who is right?’
I’ll post the source of the solution I have (I didn’t work it out myself) in a couple of weeks time.
Cheers,
Mike
Just a bit of geometry. I think the right solution is V=243r^3.
The base of the pyramid is 9r and the height is 5r.
I can write a little pdf with a more accurate solution if you want.
sorry bad typo, the height is 9r too
Hi Giulio
Thanks for having a go but I fear you are incorrect also.
The solution I have evaluates to 226.195 r^3 but I have it in closed form.
Now, it’s not my solution I am using. I had a go, gave up and cheated so you can still beat ME if you come up with the correct solution. My source is old but reliable ;)
keep it up guys!
I get the answer but my approach I used is not pretty
but my approach I used is not pretty
Well it’s the same as the solution I have but my approach is almost certainly less pretty (I cheated)!
Nice one :)
Mike,
Are you going to post the solution? If so, and if it’s as ugly as my solution, I’ll send you what I did. I could not see any neat geometrical proof as alluded to by the other attempted solutions, and given the answer I doubt there is one.
kiwi
Hi Kiwi
I’m going to post the source of ‘my’ solution which is freely available so everyone will be able to read it.
Watch this space.
Cheers,
Mike
Hi Mike,
Could you give us a hint such us on whether the solution in the source you have seen derives the equation of the tangential planes to the spheres?
Best,
Américo
Hi Américo
All will be revealed this week.
Mike
I get [(194 + 280sqrt2)/3]r^3. The tricky part is visualizing the square base which is a bit larger than one might think at first. It’s not 8r by 8r. This makes sense if you think about the lateral faces of the pyramid slanting out as they go down. I drew a cross section of the pyramid that would slice through the top vertex and the base diagonally through two opposite vertices. Then I thought in terms of 45-45-90 triangles in which the hypotenuse is 2r (could be inscribed in one semicircle). By doing this, I noticed that the height was 4sqrt2r + 1r and side of square base 8r + sqrt2r. Then use the formula for volume of pyramid, (1/3)Bh. Am I right?
Don
Hi Don
The solution is at
http://www.walkingrandomly.com/?p=1435
Cheers,
Mike