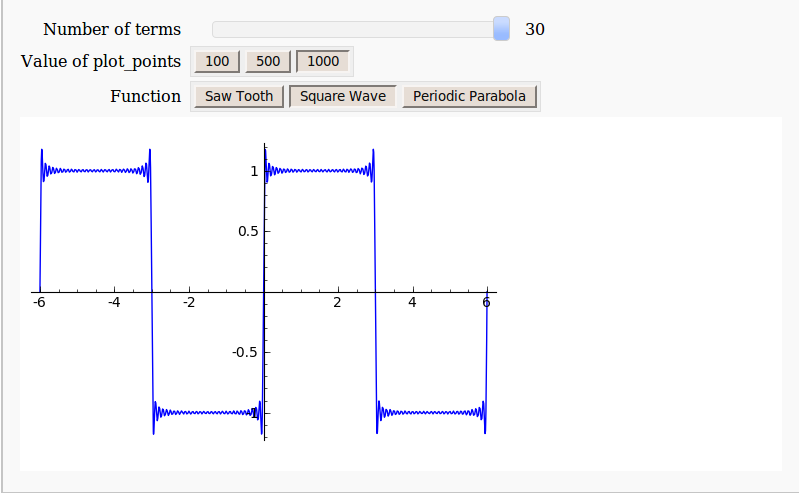
Archive for the ‘general math’ Category
If you have an interest in mathematics, you’ve almost certainly stumbled across The Wolfram Demonstrations Project at some time or other. Based upon Wolfram Research’s proprietary Mathematica software and containing over 8000 interactive demonstrations, The Wolfram Demonstrations Project is a fantastic resource for anyone interested in mathematics and related sciences; and now it has some competition.
Sage is a free, open source alternative to software such as Mathematica and, thanks to its interact function, it is fully capable of producing advanced, interactive mathematical demonstrations with just a few lines of code. The Sage language is based on Python and is incredibly easy to learn.
The Sage Interactive Database has been launched to showcase this functionality and its looking great. There’s currently only 31 demonstrations available but, since anyone can sign up and contribute, I expect this number to increase rapidly. For example, I took the simple applet I created back in 2009 and had it up on the database in less than 10 minutes! Unlike the Wolfram Demonstrations Project, you don’t need to purchase an expensive piece of software before you can start writing Sage Interactions….Sage is free to everyone.
Not everything is perfect, however. For example, there is no native Windows version of Sage. Windows users have to make use of a Virtualbox virtual machine which puts off many people from trying this great piece of software. Furthermore, the interactive ‘applets’ produced from Sage’s interact function are not as smooth running as those produced by Mathematica’s Manipulate function. Finally, Sage’s interact doesn’t have as many control options as Mathematica’s Manipulate (There’s no Locator control for example and my bounty still stands).
The Sage Interactive Database is a great new project and I encourage all of you to head over there, take a look around and maybe contribute something.
In a recent tweet, Cliff Pickover told the world that
727272727272727272727272727272727272727272727272727272727272727272727272727272727272727272727272727 is prime. That’s a nice looking prime and it took my laptop 1/100th of a second to confirm using Mathematica 8.
PrimeQ[727272727272727272727272727272727272727272727272727272727272727\
272727272727272727272727272727272727] // AbsoluteTiming
Out[1]= {0.0100000, True}
Can anyone else suggest some nice looking primes?
It is possible to write many integers as the sum of the cubes of three integers. For example
99 = (-5)^3 + 2^3+ 6^3
A more complicated example is
91 = (-67134)^3 + (-65453)^3+(83538)^3
Your task is to find integers x,y and z such that
33 = x^3 + y^3 + z^3
Hint: This is not a trivial problem and will (probably) require the use of a computer. Extra credit given if you also post your source code.
Update 3: If you are serious about attempting to crack this problem (and some people seem to be, judging from the comments), the following reference may be of help. The bibliography includes other jumping off points for this problem.
- Michael Beck, Eric Pine, Wayne Tarrant and Kim Yarbrough Jensen: New integer representations as the sum of three cubes Math. Comp. 76 (2007), 1683-1690 (Link)
Update 2: This problem is, in fact, a long-standing unsolved problem in number theory. If my memory serves me correctly, it is mentioned in the book Unsolved Problems in Number Theory
Update 1: 33 is very VERY difficult so why not use 16 as a warm up problem. MUCH smaller search space.
A friend recently asked me how to optimally tile the shape below on the plane such that no two instances touch.

Off the top off my head I suggested considering the minimal enclosing circle and then pack hexagonally but he thinks one could do better. I thought I’d ask on here to see what others might come up with.
I work in a beautiful old building at The University of Manchester called The Sackville Street Building. Yesterday, I took part in a very interesting historical tour of the building and was astonished at the amount of beautiful things that I had never noticed before and yet walk past every day.
For example, I was delighted to discover that one of the stained glass windows in the great hall was themed around mathematics (thanks to Samantha Bradey for the original image which I’ve heavily compressed for this blog post)

While on the tour I posted a quick snap of the above window to twitter using my mobile phone and received some nice feedback along with a few pictures of other mathematical windows. It turns out that Manchester’s Nick Higham has a close up of the above window for example. Also, Kit Yates tweeted about several mathematical windows in Caius College, Cambridge, one of which is below (showing images related to Venn and Fisher).

Do you know of any other examples of mathematics in stained glass? Feel free to contact me and tell me all about it.
My attention was recently drawn to a Google+ post by JerWei Zhang where he evaluates 2^3^4 in various packages and notes that they don’t always agree. For example, in MATLAB 2010a we have 2^3^4 = 4096 which is equivalent to putting (2^3)^4 whereas Mathematica 8 gives 2^3^4 = 2417851639229258349412352 which is the same as putting 2^(3^4). JerWei’s post gives many more examples including Excel, Python and Google and the result is always one of these two (although to varying degrees of precision).
What surprised me was the fact that they disagreed at all since I thought that the operator precendence rules were an agreed standard across all software packages. In this case I’d always use brackets since _I_ am not sure what the correct interpretation of 2^3^4 should be but I would have taken it for granted that there is a standard somewhere and that all of the big hitters in the numerical world would adhere to it.
Looks like I was wrong!
Consider a periodic sequence, seqp, with period p
seqp = a1, a2, …, ap, a1, a2, …, ap, a1, a2, …, ap, …
Two sub-sequences, each of length N where 2< N< p, are produced by choosing two random start points in seqp and using the next N-1 numbers. What is the probability that these two sub-sequences will overlap?
If you take M>2 such length N sub-sequences then what is the probability that any two will overlap?
For a more concrete example, assume that p = 2^19937 – 1 (yes, a very big number) and consider 10,000 sub-sequences each of length 10^9.
Disclaimer: I don’t have the solution to this and haven’t yet tried to find it
Consider this indefinite integral
![]()
Feed it to MATLAB’s symbolic toolbox:
int(1/sqrt(x*(2 - x))) ans = asin(x - 1)
Feed it to Mathematica 8.0.1:
Integrate[1/Sqrt[x (2 - x)], x] // InputForm (2*Sqrt[-2 + x]*Sqrt[x]*Log[Sqrt[-2 + x] + Sqrt[x]])/Sqrt[-((-2 + x)*x)]
Let x=1.2 in both results:
MATLAB's answer evaluates to 0.2014 Mathematica's answer evaluates to -1.36944 + 0.693147 I
Discuss!
Matt Tearle has produced a MATLAB version of my Interactive Slinky Thing which, in turn, was originally inspired by a post by Sol over at Playing with Mathematica. Matt adatped the code from some earlier work he did and you can click on the image below to get it. Thanks Matt!
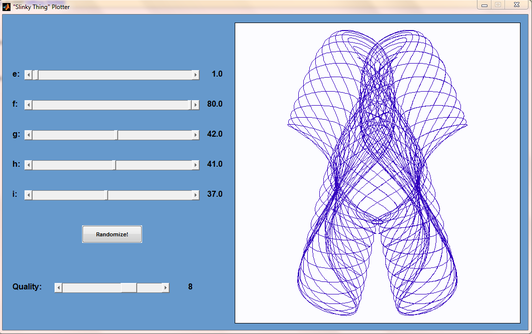
Over at Playing with Mathematica, Sol Lederman has been looking at pretty parametric and polar plots. One of them really stood out for me, the one that Sol called ‘Slinky Thing’ which could be generated with the following Mathematica command.
ParametricPlot[{Cos[t] - Cos[80 t] Sin[t], 2 Sin[t] - Sin[80 t]}, {t, 0, 8}]
Out of curiosity I parametrised some of the terms and wrapped the whole thing in a Manipulate to see what I could see. I added 5 controllable parameters by turning Sol’s equations into
{Cos[e t] - Cos[f t] Sin[g t], 2 Sin[h t] - Sin[i t]}, {t, 0, 8}
Each parameter has its own slider (below). If you have Mathematica 8, or the free cdf player, installed then the image below will turn into an interactive applet which you can use to explore the parameter space of these equations.
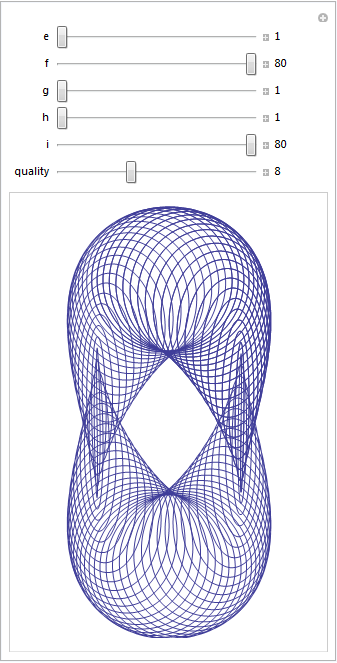
Here are four of my favourites. If you come up with one that you particularly like then feel free to let me know what the parameters are in the comments.